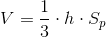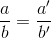Ostrosłupy
Stronę tą wyświetlono już: 22180 razy
Definicja ostrosłupa
Ostrosłupem jest każda bryła, której ściany boczne są trójkątami a jej podstawa wielokątem dowolnym. Wśród ostrosłupów wyróżnia się następujące grupy:
- ostrosłupy prawidłowe, których podstawa jest wielokątem foremnym a punkt przecięcia prostej prostopadłej do płaszczyzny podstawy przechodzącej przez wierzchołek tego ostrosłupa znajduje się w środku ciężkości podstawy, lub ściślej rzecz ujmując w środku okręgu opisanego na podstawie. Ściany boczne ostrosłupa prawidłowego są przystającymi trójkątami równoramiennymi;
- ostrosłup pochyły - to taki, w którym prosta prostopadła do płaszczyzny podstawy przechodząca przez wierzchołek ostrosłupa nie przecina podstawy w środku jej ciężkości;
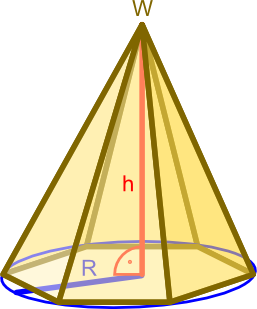
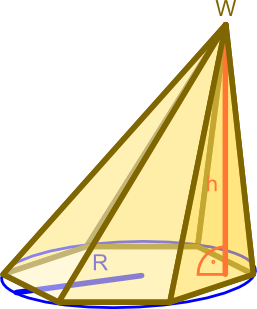
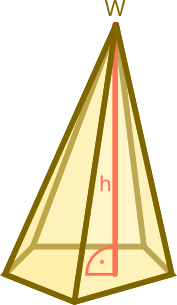
Oznaczenia
- h - wysokość ostrosłupa;
- R - promień okręgu opisanego na wielokącie foremnym.
ostrosłupy mające w podstawie n-kąt foremny nazywa się ostrosłupem n-kątnym.
Podstawowe wzory:
Wzory ogólne:
Objętość ostrosłupa dowolnego można obliczyć z następującego wzoru:
gdzie:
- h - wysokość ostrosłupa;
- Sp - pole powierzchni podstawy.
Ostrosłypy o podstawie trójkąta (czworościany)
Wzory dla czworościanów, które jednocześnie są ostrosłupami można znaleźć na stronie Matematyka → Geometria → Czworościany.
Ostrosłupy o podstawie równoległościanu:
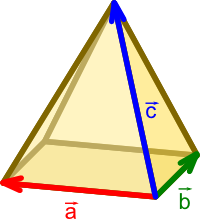
Jeżeli dane są trzy wektory a, b i c to objętość ostrosłupa o podstawie równoległoboku można obliczyć z wzoru następującej postaci:
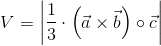 | [2] |
Zapis wyrażenia w formacie TeX-a:
Definicja ostrosłupa ściętego:
Ostrosłupem ściętym jest to ostrosłup, który został ścięty płaszczyzną równoległą do podstawy na wysokości h. Płaszczyzna powstała w ten sposób jest wielokątem podobnym do wielokąta podstawy, co z kolei oznacza, że stosunek odpowiednich dwóch boków podstawy górnej do odpowiadających im dwóch boków podstawy dolnej są sobie równe.
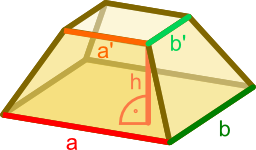
Oznaczenia:
- a, b - długości boków podstawy dolnej";
- a', b' - długości boków podstawy górnej;
- h - wysokość ostrosłupa ściętego
Na powyższej ilustracji zaznaczone długości boków podstaw muszą spełniać następującą równość, aby taka bryła mogła mieć zaszczyt nazywania się ostrosłupem ściętym:
W każdym ostrosłupie ściętym boki są trapezami.
Obliczanie objętości dowolnego ostrosłupa ściętego
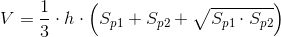 | [4] |
Zapis wyrażenia w formacie TeX-a:
gdzie:
- h - wysokość ostrosłupa ściętego;
- Sp1, Sp2 - pola powierzchni podstaw.