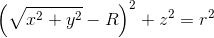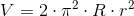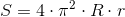Torusy

Autor podstrony: Krzysztof Zajączkowski

Stronę tą wyświetlono już: 8071 razy

Definicja torusa

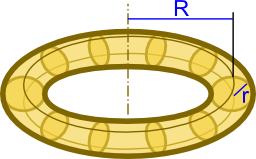
Torus jest to bryła obrotowa powstała w wyniku obrotu płaszczyzny koła względem osi leżącej na płaszczyźnie tego koła lecz nie mającej punktów wspólnych z nim.

Rys. 1
Ilustracja torusa wraz z oznaczeniami:
R - promień obrotu płaszczyzny okręgu tworzącej torus;

r - promień okręgu, będącego przekrojem osiowym torusa;

Równanie torusa

Płaszczyznę torusa opisuje następująca równość:

[1]

Zapis wyrażenia w formacie TeX-a:

\left(\sqrt{x^2 + y^2} - R\right)^2 + z^2 = r^2

Parametryczne równanie torusa dla kątów α - kąta położenia punktu na obwodzie koła przekroju torusa i β kąta obrotu płaszczyzny tworzącej torusa.

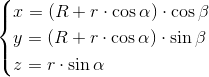[2]

Zapis wyrażenia w formacie TeX-a:

\begin{cases}x=(R+r\cdot\cos \alpha)\cdot\cos \beta \\ y=(R+r\cdot\cos \alpha)\cdot\sin \beta \\ z=r\cdot \sin \alpha\end{cases}

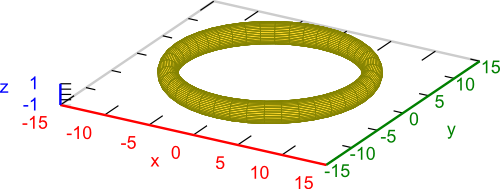
Poniżej zamieszczony został wykres torusa utworzony w programie wxMaxima z wykorzystaniem powyższego wzoru.

Wykres torusa uzyskany w programie wxMaxima — Rys. 2
Wykres torusa uzyskany w programie **wxMaxima** za pomocą następującego kodu:
plot3d([(R+r*cos(x))*cos(y), (R+r*cos(x))*sin(y), r*sin(x)], [x, 0, 2*%pi], [y, 0, 2*%pi], [grid, 40,40],[azimuth, 30],[elevation, 10],[palette,[value,float(35 / 255),float(213/255),float(255/255),0.9]], [gnuplot_term, "svg size 500, 250"], [gnuplot_out_file, "C:\\Torus_wxMaxima.svg"]);

Plik został wyeksportowany do formatu **png** i edytowany w programie **Inkscape**

Podstawowe wzory

Objętość torusa

Objętość torusa jest równa iloczynowi obwodu okręgu o promieniu R i pola powierzchni koła o promieniu r:

[3]

Zapis wyrażenia w formacie TeX-a:

V=2\cdot \pi\cdot R\cdot r^2

Pole powierzchni torusa

Pole powierzchni torusa odpowiada polu powierzchni bocznej walca o podstawie okręgu o promieniu r i wysokości h tegoż walca równej 2·π·R.

[4]

Zapis wyrażenia w formacie TeX-a:

S=4\cdot\pi^2\cdot R\cdot r