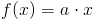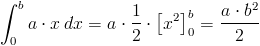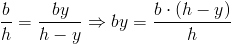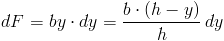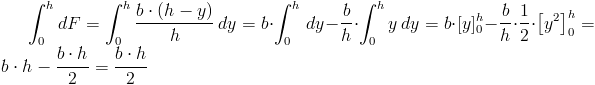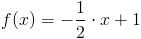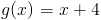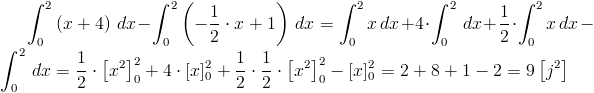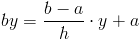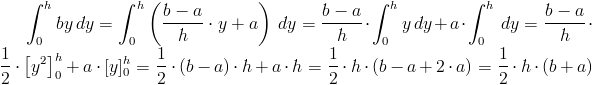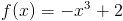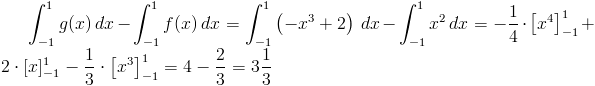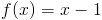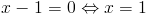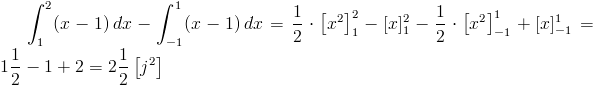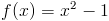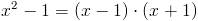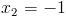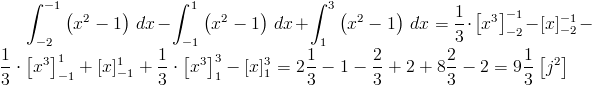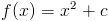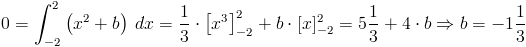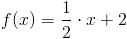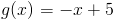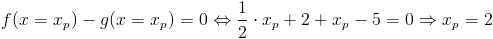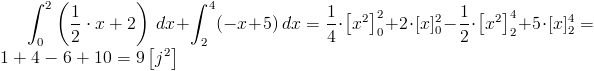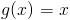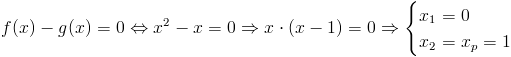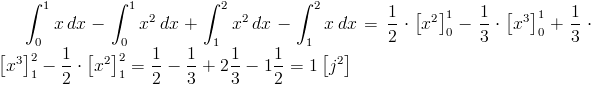Obliczanie pola powierzchni

Stronę tą wyświetlono już: 7348 razy

Zadanie 1 Wyznaczyć wzór na pole powierzchni trójkąta prostokątnego opisanego funkcją:

w przedziale od 0 do b.

Rozwiązanie:

Parametr a funkcji jest równy tan α, gdzie α to wartość kąta zawartego pomiędzy osią x a wykresem funkcji f(x). Z kolei b jest długością boku trójkąta prostokątnego. W ten oto prosty sposób wyprowadzony został wzór na pole powierzchni trójkąta prostokątnego w zależności od danych tan α=a, b.

Zadanie 2 Wyprowadzić wzór na pole powierzchni trójkąta prostokątnego, którego długości boków przyprostokątnych b, h są dane.

Rozwiązanie:

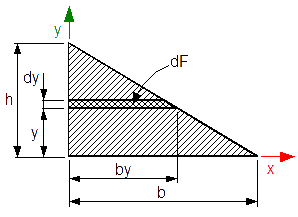
Pole powierzchni trójkąta jest równe sumie elementarnych pól powierzchni dF, których szerokość by jest uzależniona od położenia y danego przekroju elementarnego oraz długości b, h opisujących wymiary danego trójkąta. Zależność wymiaru by od wspomnianych już wcześniej parametrów jest więc następująca:

Elementarne pole powierzchni dF jest równe:

Ostatecznie więc wzór na pole powierzchni danego trójkąta:

Dla lepszego zrozumienia warto zerknąć łaskawym okiem na rysunek 1, gdzie wszystkie dane zostały rozpisane graficznie. Wyprowadzony wzór jest również prawdziwy dla wszystkich trójkątów, pod warunkiem że h jest wysokością danego trójkąta spuszczoną prostopadle na bok b z przeciwległego wierzchołka.

Zadanie 3 Obliczyć pole powierzchni trapezu zawartego pomiędzy funkcjami:

w przedziale od 0 do 2.

Rozwiązanie:

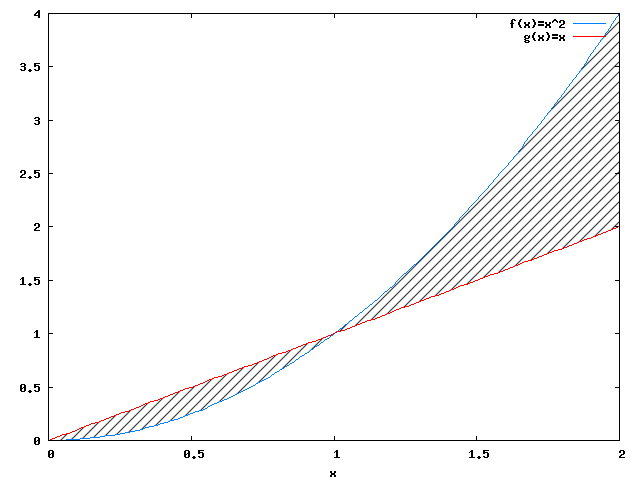
Należy zacząć od nakreślenia funkcji f(x), g(x) w zadanym przedziale wartości.

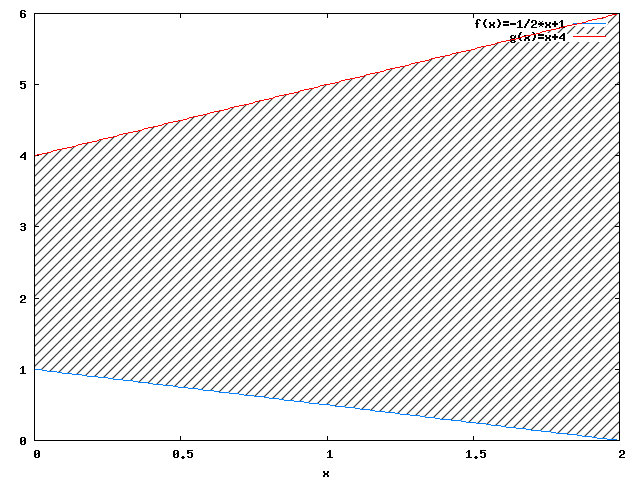
Jak widać na załączonym rysunku 2 pole powierzchni trapezu zawartego między funkcjami f(x), g(x) jest równe różnicy całek oznaczonych z tychże funkcji w przedziale od 0 do 2:

Zadanie 4 Wyprowadzić wzór na pole powierzchni trapezu o danych długościach boków a, b oraz wysokości h.

Rozwiązanie:

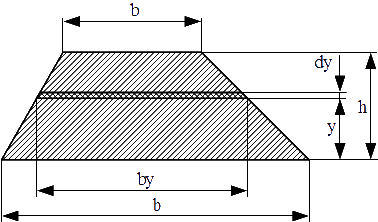
Z rysunku 5 wynika, że elementarne pole powierzchni dF jest równe iloczynowi by⋅dy. Wartość by trzeba uzależnić od zmiennej y oraz wymiarów boków a, b oraz wysokości h trapezu w następujący sposób:

Podstawiając powyższą zależność za by można wyprowadzić wzór na pole powierzchni trapezu:

I wzór na pole powierzchni trapezu o danych długościach boków a, b oraz wysokości h został wyprowadzony.

Zadanie 5 Obliczyć pole powierzchni figury zawartej pomiędzy funkcjami:

w przedziale od -1 do 1.

Rozwiązanie:

Zerkając łaskawym okiem na wykres z rysunku 4 z łatwością można stwierdzić, że od całki funkcji g(x) trzeba odjąć całkę z funkcji f(x).

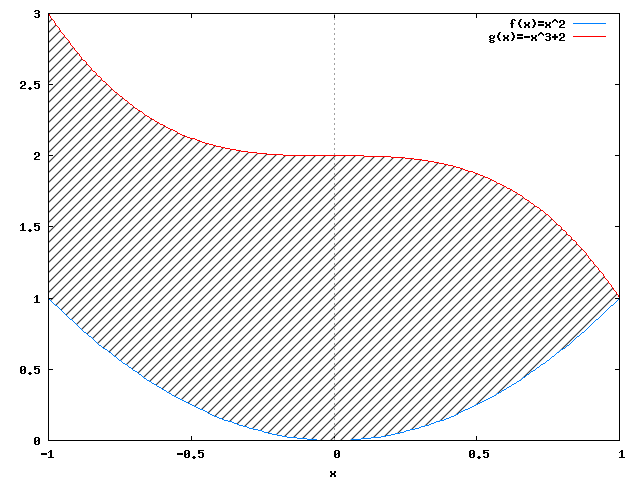
Przystąpmy więc do rozwiązania zadania:

Zadanie 6 Obliczyć pole powierzchni zawartej pomiędzy osią x a funkcją:

w przedziale od -1 do 2.

Rozwiązanie:

Z rysunku 5 wynika, że funkcja f(x) ma miejsce zerowe w przedziale całkowania. Oznacza to, że konieczne będzie podzielenie przedziału całkowania na dwie części: pierwszą od -1 do x₀ oraz drugą od x₀ do 2.

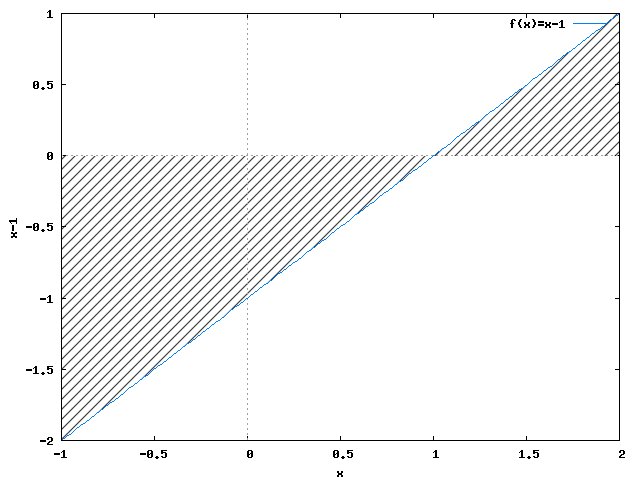
Miejsce zerowe funkcji f(x) wyznaczyć należy:

Miejsce zerowe funkcji f(x) znajduje się w punkcie x₀=1, więc zgodnie z wcześniej omówionym planem podziału przedziału całkowania na dwie części obliczyć trzeba pole powierzchni odejmując od całki po przedziale <x₀,2> całkę po przedziale <-1,x₀>.

Zadanie 7 Obliczyć pole powierzchni figury zawartej pomiędzy osi x a wykresem funkcji:

w przedziale od -2 do 3.

Rozwiązanie:

Na rysunku 6 widać, że funkcja f(x) przebiega poniżej jak i powyżej osi x. Z tego względu konieczne jest rozbicie przedziału całkowania na trzy części: pierwszą od -2 do x₁, drugą od x₁ do x₂ oraz trzecią od x₂ do 3, gdzie x₁, x₂ - miejsca zerowe funkcji f(x).

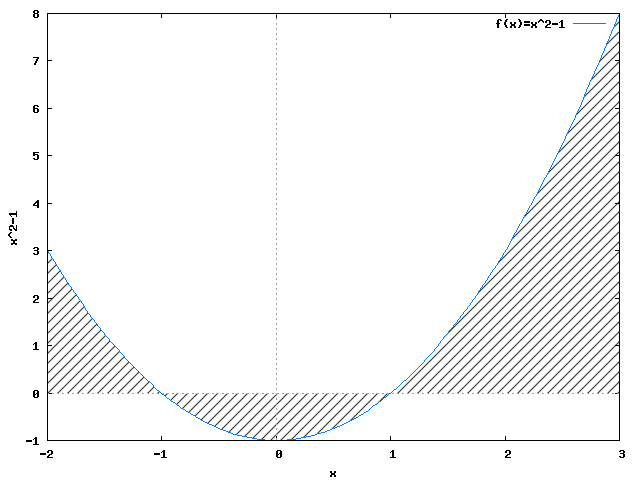
Postać iloczynową funkcji f(x) można zapisać stosując wzór skróconego mnożenia:

więc miejsca zerowe mają następujące wartości:

Obliczenie pola powierzchni figury leżącej między funkcją f(x) a osią x:

Zadanie 8 Wyznaczyć wartość parametru c funkcji

tak aby pole powierzchni części wykresu tej funkcji znajdującej się nad osią x było równe polu powierzchni wykresu funkcji znajdującego się pod osią x w przedziale od -2 do 2.

Rozwiązanie:

Należy scałkować funkcję f(x) i znaleźć taką wartość parametru c, dla której owa całka jest równa zero. Wystarczy więc rozwiązać następujące równanie:

Wykres funkcji f(x) dla b=-1.(3) można obejrzeć na rysunku 7.

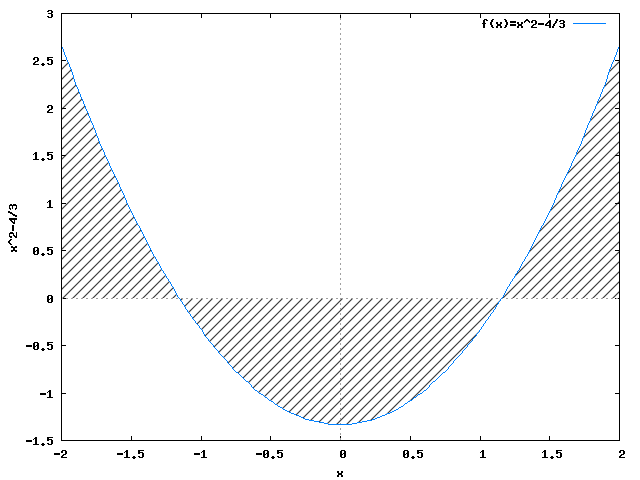
Zadanie 9 Obliczyć pole powierzchni zawartej pomiędzy funkcją

a osią x od 0 do przecięcia z funkcją

oraz pole powierzchni pod funkcją g(x) od punktu przecięcia z funkcją f(x) do 4.

Rozwiązanie:

Rozwiązaniem będzie suma całek funkcji f(x) w przedziale od 0 do x_p oraz g(x) w przedziale od x_p do 4 co wynika z rysunku 8. Oczywiście x_p to nic innego jak punkt przecięcia się funkcji f(x), g(x).

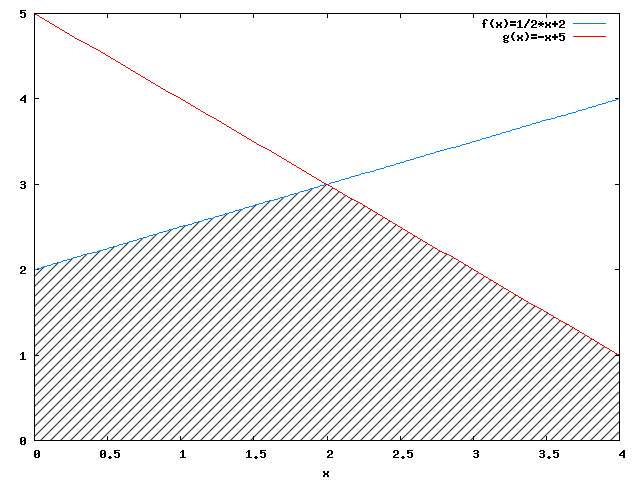
Wyznaczenie punktu przecięcia się funkcji f(x), g(x):

Obliczenie pola powierzchni:

Zadanie 10 Obliczyć pole powierzchni figury znajdującej się pomiędzy funkcją:

a funkcją:

w przedziale od 0 do 2.

Rozwiązanie:

Niestety funkcje f(x), g(x) w przedziale całkowania się przecinają (co można zobaczyć na rysunku 9) w związku z czym konieczny jest podział przedziału całkowania na dwie części: pierwszą od 0 do x_p będącą różnicą całki z funkcji g(x) i f(x), oraz drugą od x_p do 2 będącą różnicą całki z funkcji f(x) i g(x).

Wyznaczenie punktów przecięcia funkcji f(x) z funkcją g(x):

Obliczenie pola powierzchni: