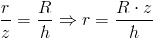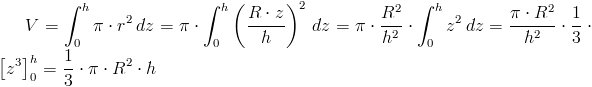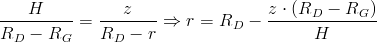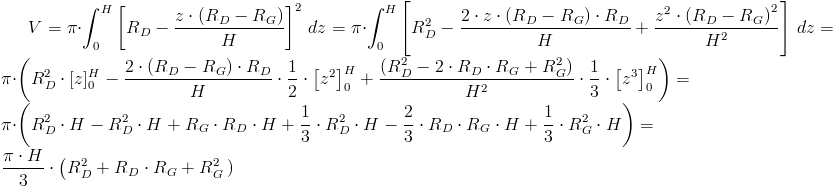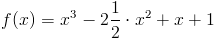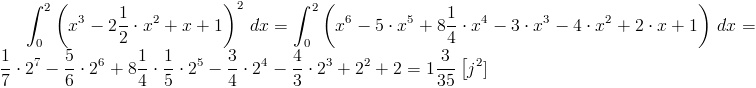Stronę tą wyświetlono już: 6744 razy

Zadanie 1 Wyznaczyć wzór na objętość stożka o danej wysokości h oraz promieniu podstawy R.

Rozwiązanie:

Zerkając łaskawym okiem na rysunek 1 można zapisać następujący ogólny wzór na objętość stożka:

gdzie:

• π⋅r² dz - elementarna objętość dV.

Parametr r trzeba uzależnić od położenia danej objętości elementarnej dV od jego położenia z w następujący sposób:

Podstawienie i wyprowadzenie:

Zadanie 2 Wyznaczyć wzór na objętość stożka ściętego o danej wysokości h oraz promieniach R_g, R_d.

Rozwiązanie:

Jak w zadaniu 1 tak i tutaj obowiązuje wzór ogólny na objętość tym razem stożka ściętego:

gdzie:

• π⋅r² dz - elementarna objętość dV.

Promień r trzeba uzależnić od wymiarów stożka R_d, R_g oraz h jak również od położenia danej objętości elementarnej dV na osi z.

Podstawienie i wyprowadzenie:

Zadanie 3 Obliczyć objętość bryły obrotowej o zarysie funkcji

w przedziale od 0 do 2

Rozwiązanie:

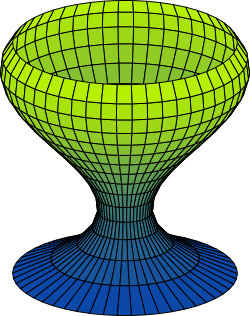
Poprzez obrót powierzchni z rysunku 3 powstaje bryła, której zarys można obejrzeć z kolei na rysunku 4. Objętość bryły można obliczyć korzystając z wzoru [2] z strony Matematyka → Całki oznaczone → Podstawowe wzory.

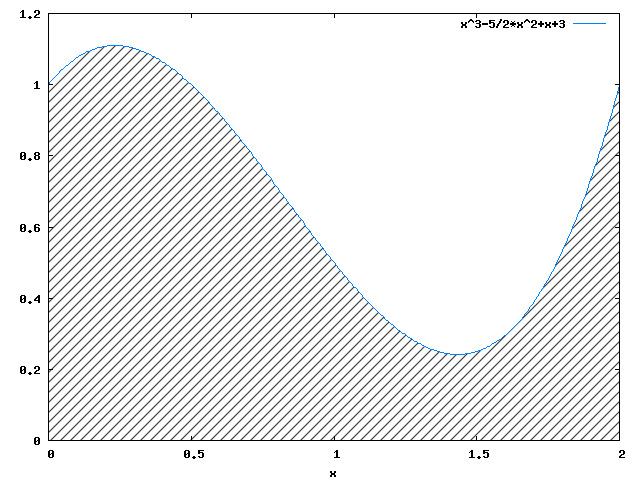
Obliczenie objętości danej bryły obrotowej:

Przyjmując jako jednostkę cm można śmiało stwierdzić, że bryłka ma niewielką objętość.