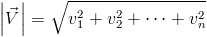Stronę tą wyświetlono już: 8193 razy

Wektorem nazywa się zbiór uporządkowanych liczb przestrzeni n-wymiarowej, gdzie n - określa wielkość zbioru liczb wektora. Najczęściej spotykane i używane są wektory 2W i 3W, stanowiące opis położenia, przemieszczenia, prędkości, przyspieszenia lub innej wielkości wektorowej. Wektory zawierają w sobie informacje o: kierunku, zwrocie, składowych wypadkowych danej wielkości fizycznej oraz wartości wektora, przy czym każdy wektor można sprowadzić do wartości liczbowej (skalara), która jest w stanie określić jedynie wartość wektora.

Typowe przykłady wektorów 2W oraz 3W:

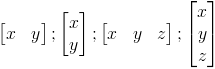Zapis wyrażenia w formacie TeX-a:

\begin{bmatrix} x & y \end{bmatrix}; \begin{bmatrix} x\\ y \end{bmatrix};\begin{bmatrix}x & y & z\end{bmatrix};\begin{bmatrix} x\\ y\\ z \end{bmatrix}

Jak już wcześniej była o tym mowa, wektory charakteryzują się pewnymi własnościami, do których należą:

kierunek wektora - prosta, na której wektor leży;
• zwrot wektora - określa, w kierunku którego końca prostej wektor jest skierowany;
• wartość wektora - określa długość wektora, która z kolei dana jest następującą zależnością:

  [1]

  Zapis wyrażenia w formacie TeX-a:

  \left|\vec{V}\right|=\sqrt{v_1^2+v_2^2+\cdots+v_n^2}

  Wzór [1] jest ściśle powiązany z twierdzeniem Pitagorasa, które omówione zostało w dziale Matematyka → Geometria → Twierdzenie Pitagorasa.

Graficzną interpretację owych własności wektorów można obejrzeć na rysunku 1.

W układzie kartezjańskim wektor 2W jest opisany przez składowe x i y ale istnieje możliwość opisu tegoż wektora w układzie biegunowym za pomocą wartości W wektora oraz kąta α jego położenia. W przypadku wektorów 3W jest to wartość W wektora oraz para kątów α i β (współrzędne sferyczne).