Stronę tą wyświetlono już: 3273 razy

Iloczyn wektora a przez liczbę k jest operacją polegającą na przemnożeniu składowych wektora a przez tą liczbę w następujący sposób:

[1]

Zapis wyrażenia w formacie TeX-a:

vec{a}=vec{b}cdot k=\begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix}\cdot k=\begin{bmatrix} b_1\cdot k \\ b_2\cdot k \\ \vdots \\ b_n \cdot k \end{bmatrix}

gdzie:

• b₁, b₂, ... , b_n - składowe wektora b;
• b₁⋅k, b₂⋅k, ... , b_n⋅k - składowe wektora a.

Własności iloczynu wektora przez liczbę:

• wektory a, b mają zawsze ten sam kierunek;
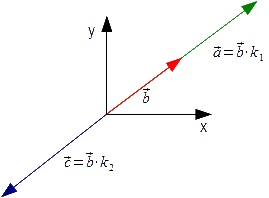
• wektory a, b mają ten sam zwrot gdy k>0 (wektor a na rysunku 1), a przeciwny gdy k<0 (wektor c na rysunku 1);
• stosunek długości wektora b do wektora a są równe liczbie k.

Dzielenie wektora przez liczbę k jest oczywiście niczym innym jak przemnożeniem nieszczęsnego wektora przez k^-1 w następujący sposób:

[2]

Zapis wyrażenia w formacie TeX-a:

\vec{a}=\vec{b}\cdot \frac{1}{k}=\begin{bmatrix}b_1 \\ b_2 \\ \vdots \\ b_n \end{bmatrix}\cdot \frac{1}{k}=\begin{bmatrix}\cfrac{b_1}{k} \\ \cfrac{b_2}{k} \\ \vdots \\ \cfrac{b_n}{k}\end{bmatrix}

gdzie:

• b₁, b₂, ... , b_n - składowe wektora b;
• b₁⋅k^-1, b₂⋅k^-1, ... , b_n⋅k^-1 - składowe wektora a.

Za pomocą mnożenia wektora przez wartość można tak przeskalować dowolny wektor a, aby jego długość była równa obranej wartości L poprzez podzielenie wektora a przez jego długość i pomnożenie przez L w następujący sposób:

[3]

Zapis wyrażenia w formacie TeX-a:

\vec{b}=\vec{a}\cdot \frac{L}{\left|\vec{a}\right|} =\begin{bmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{bmatrix}\cdot \frac{L}{\left|\vec{a}\right|}=\begin{bmatrix} a_1\cdot \cfrac{L}{\left|\vec{a}\right|} \\ a_2\cdot \cfrac{L}{\left|\vec{a}\right|} \\ \vdots \\ a_n\cdot \cfrac{L}{\left|\vec{a}\right|}\end{bmatrix}

gdzie:

• a₁, a₂, ... , a_n - składowe wektora a;
• a₁⋅L⋅|a|^-1, a₂⋅L⋅|a|^-1, ... , a_n⋅L⋅|a|^-1 - składowe wektora b.

Dzieląc wektor przez jego długość uzyskuje się wektor jednostkowy, będący wektorem o długości równej 1. Mnożąc taki wektor przez L otrzymuje się więc wektor o długości L.