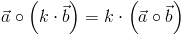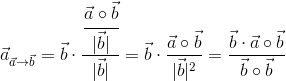Stronę tą wyświetlono już: 7521 razy

Definicja iloczynu skalarnego

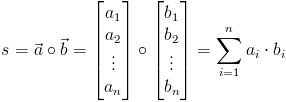
Iloczynem skalarnym dwóch wektorów jest liczba obliczana w następujący sposób:

[1]

Zapis wyrażenia w formacie TeX-a:

s=vec{a}circvec{b}=\begin{bmatrix} a_1\\ a_2\\ \vdots \\ a_n \end{bmatrix}\circ\begin{bmatrix} b_1\\ b_2\\ \vdots \\ b_n \end{bmatrix}=\sum_{i=1}^{n}a_i\cdot b_i

gdzie:

• a₁, a₂, ... , a_n - składowe wektora a;
• b₁, b₂, ... , b_n - składowe wektora b;
• s - wartość liczbowa otrzymana z iloczynu skalarnego wektorów a, b.

Interpretacja graficzna i powiązanie iloczynu skalarnego z długościami wektorów i wartością kąta zawartego między nimi

Iloczyn skalarny jest ściśle powiązany z długościami wektorów a, b oraz kątem α zawartym między nimi w następujący sposób:

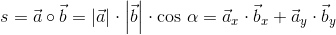[2]

Zapis wyrażenia w formacie TeX-a:

s=\vec{a}\circ\vec{b}=\left|\vec{a}\right|\cdot \left|\vec{b}\right|\cdot \cos\,\alpha=\vec{a}_x\cdot\vec{b}_x+\vec{a}_y\cdot\vec{b}_y

gdzie:

• |a|, |b| - długości wektorów a, b;
• α - kąt zawarty między wektorami a, b.

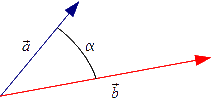
Z wzoru [2] wynika, że gdy kąt α zawarty między wektorami jest równy 90°, iloczyn skalarny wektorów równa się zero. Daje to podstawę do stwierdzenia, czy dwa wektory są prostopadłe względem siebie.

Przyrównując zależności [1], [2] stronami i odpowiednio je przekształcając można otrzymać wzór na cosinus mniejszego kąta α zawartego między danymi wektorami w następujący sposób:

[3]

Zapis wyrażenia w formacie TeX-a:

\cos\,\alpha=\frac{\vec{a}\circ \vec{b}}{\left|\vec{a}\right|\cdot \left|\vec{b}\right|}

Wartość kąta α można więc wyznaczyć w następujący sposób:

[4]

Zapis wyrażenia w formacie TeX-a:

\alpha=acos\left(\frac{a\circ b}{\left|\vec{a}\right|\cdot \left|\vec{b}\right|}\right)

Przekształcając wzór [3] można obliczyć długość rzutu wektora a na wektor b (i na odwrót) w następujący sposób:

[5]

Zapis wyrażenia w formacie TeX-a:

\left|\vec{a}\right|\cdot cos\,\alpha=\frac{\vec{a}\circ \vec{b}}{\left|\vec{b}\right|}

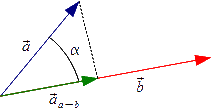
Znając długość L_a→b rzutu wektora a na wektor b daną zależnością [5] można obliczyć wektor a_a→b będący rzutem wektora a na wektor b poprzez podzielenie wektora b przez jego długość i pomnożenie go przez znaną długość rzutu L_a→b:

[6]

W mianowniku równania [6] znajduje się zapis kwadratu długości wektora b, który następnie zastąpiony został iloczynem skalarnym wektora b przez wektor b. Stało się tak, ponieważ zachodzi równość pomiędzy tymi wielkościami, którą można zapisać najogólniej w następujący sposób:

[7]

Zapis wyrażenia w formacie TeX-a:

\left|\vec{b}\right|\cdot \left|\vec{b}\right|=\vec{b}\circ \vec{b}\Rightarrow \left|\vec{b}\right|=\sqrt{\vec{b}\circ\vec{b}}

Całą operację rzutowania wektora a na wektor b można obejrzeć na rysunku 2, z którego wynika że wektor a_a→b jest równoległy do wektora b oraz jest rzutem wektora a na wektor b.

Własności operatora mnożenia skalarnego wektorów:

przemienność:

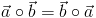
rozdzielność względem dodawania i odejmowania:

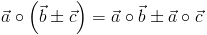
przemienność względem mnożenia wektora przez wartość liczbową: