Stronę tą wyświetlono już: 8875 razy

Macierzą nazywa się m×n wymiarową tablicę liczb, gdzie m, n∈N{0}. Przykładowe macierze o wymiarach 2×3, 3×2 (macierze prostokątne) oraz 3×3 (macierz kwadratowa):

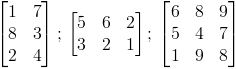Zapis wyrażenia w formacie TeX-a:

\begin{bmatrix} 1 & 7\\ 8 & 3\\ 2 & 4 \end{bmatrix};,\begin{bmatrix} 5 & 6 & 2\\ 3 & 2 & 1 \end{bmatrix};,\begin{bmatrix} 6 & 8 & 9\\ 5 & 4 & 7\\ 1 & 9 & 8 \end{bmatrix}

Ogólną postać macierzy opisuje więc następujący zapis:

[1]

Zapis wyrażenia w formacie TeX-a:

M_{m \times n}=\begin{bmatrix} a_{1,1} & a_{1,2} & a_{1,3} & \cdots & a_{1,m}\\ a_{2,1} & a_{2,2} & a_{2,3} & \cdots & a_{2,m}\\ a_{3,1} & a_{3,2} & a_{3,3} & \cdots & a_{3,m}\\ \vdots & \vdots & \vdots & \ddots & \vdots a_{n,1} & a_{n,2} & a_{n,3} & cdots & a_{n,m} \end{bmatrix}

gdzie:

• wyrażenia a_i,j są elementami lub też współczynnikami macierzy M_m×n

Zastosowanie macierzy

Szerokie zastosowanie macierzy ma miejsce w świecie algebry liniowej, a więc rozwiązywanie układów równań liniowych. Dzięki optymalnym algorytmom obliczeniowym można rozwiązywać układy równań liniowych za pomocą komputerów. Zastosowanie tego jest ogromne, ja sam miałem przyjemność wykorzystać algorytm rozwiązywania liniowych układów równań metodą eliminacji Gaussa-Jordana w programie do rozwiązywania statycznie wyznaczalnych kratownic (link do krótkiego opisu tego programu zamieszczam na końcu strony).

Również w świecie grafiki wektorowej a nawet i rastrowej macierze mają wielkie zastosowanie. Wszelkiego typu obroty, pochylenia, zniekształcenia liniowe oraz skalowania obiektów wektorowych a nawet i rastrowych wiąże się ze znajomością rachunku macierzowego i wektorowego oraz znajomości macierzowych przekształceń. W bibliotekach graficznych takich OpenGL stosuje się wbudowane mechanizmy w celu wykonywania wszelkiego typu operacji liniowo zależnych na obiektach trójwymiarowych. Wszystkie programy do grafiki wektorowej korzystają z rachunku wektorowego i macierzowego, a do tego typu oprogramowania można zaliczyć: Inkscap-a, Kerkythe-ę, Blender-a, 3D Max Studio, AutoCad-a, Kati-ę, Solid Works-a, Google Sketch Up-a, Corel Draw-a

Organizacja danych bitmapowych wyświetlanych na ekranach komputerów jest realizowana w sposób jak najbardziej macierzowy, jednakże w pamięci komputera bitmapa jest zapisywana w postaci macierzy o wymiarze 1×n, gdzie n∈N{0}.

Strony powiązane

Darmowy kurs macierzowy Mateusza Kowalskiego