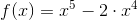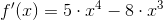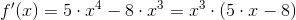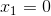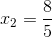Ekstrema funkcji i mafijne ich powiązanie z pochodną funkcji
Stronę tą wyświetlono już: 2436 razy
Ekstremo funkcji to nic innego jak taki punkt na wykresie funkcji f(x), którego kąt pomiędzy styczną do tegoż punktu wykresu funkcji f(x) a osią x jest równy zero. Taki punkt wyznacza: minimum globalne lub minimum lokalne lub minimum globalne lub maksimum lokalne funkcji f(x). Jaką więc wartość pochodnej w tymże punkcie musi mieć funkcja f(x) aby punkt był ekstremum funkcji? No pochodna to tangens kąta stycznej do punktu wykresu f(x) a więc wszystkie znaki na Ziemi i na niebie mówią zgodnie, że zerowa musi być wartość ta, albowiem tangens 0° jest równy 0. Innymi słowy szukanie ekstrema polega na znalezieniu miejsc zerowych pochodnej f'(x) funkcji f(x). Jeżeli pochodna tejże funkcji nie ma miejsc zerowych to nie ma również ekstrema.
Weźmy na warsztat taką oto funkcję, której ekstrema należy wyznaczyć:
Wykres tej funkcji w interesującym mnie przedziale od -1 do 2.2 pokazany został na poniższej ilustracji.
Obliczanie pierwszej pochodnej:
Z najdzikszą rozkoszą nanoszę ją na wykres.
Wyznaczanie miejsc zerowych funkcji f'(x):
a więc pierwsze miejsce zerowe:
i drugie miejsce zerowe:
Rzućmy łaskawym okiem na poniższy wykres, gdzie naniesione zostały niezbędne oznaczenia. Widać, że miejsca zerowe pochodnej f'(x) zaznaczone zieloną pionową linią pokrywają się z ekstremami funkcji f(x). Z wykresu można stwierdzić, że w punkcie x1=0 znajduje się maksimum lokalne funkcji f(x) zaś w punkcie x2 znajduje się minimum lokalne funkcji f(x).

Tytuł:
Matematyka w uczeniu maszynowym
Autor:
Marc Peter Deisenroth, A. Aldo Faisal, Cheng Soon Ong

Tytuł:
Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie
Autor:
Ryan T. White, Archana Tikayat Ray

Tytuł:
Matematyka w Pythonie. Algebra, statystyka, analiza matematyczna i inne dziedziny
Autor:
Amit Saha

Tytuł:
Matematyka dla menedżerów. Wydanie II
Autor:
Michael C. Thomsett

Tytuł:
Matematyka Poradnik encyklopedyczny
Autor:
I.N. Bronsztejn, K.A. Siemiendiajew

Tytuł:
Matematyka finansowa
Autor:
Jacek Jakubowski, Andrzej Palczewski, Marek Rutkowski, Łukasz Stettner

Tytuł:
Proste jak pi Matematyka to bułka z masłem
Autor:
Liz Strachan

Tytuł:
O twierdzeniach i hipotezach. Matematyka według Delty
Autor:
Witold Sadowski, Wiktor Bartol

Tytuł:
Matematyka dla biologów
Autor:
Dariusz Wrzosek

Tytuł:
Matematyka dla programistów Java
Autor:
Jacek Piechota