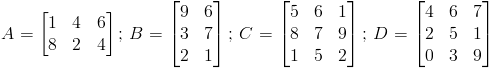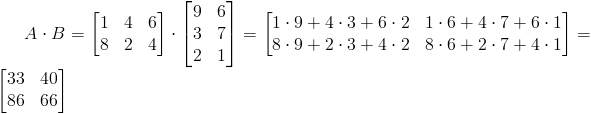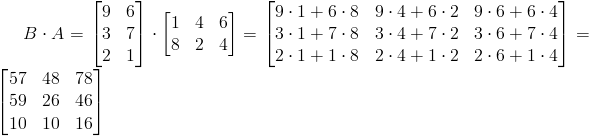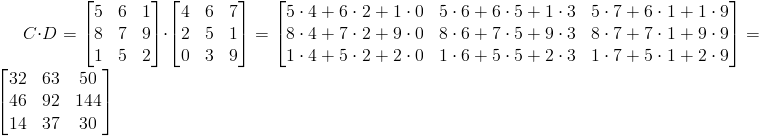Mnożenie macierzy przez macierz
Stronę tą wyświetlono już: 2769 razy
Mnożenie macierzy jest możliwe jedynie w przypadku, gdy dana macierz A ma tyle samo kolumn co macierz B wierszy. Ogólny zapis mnożenia dwóch macierzy wygląda więc następująco:
![Równanie [1]](https://www.obliczeniowo.com.pl/rownania/w_1135.gif) | [1] |
Zapis wyrażenia w formacie TeX-a:
A\cdot B=\begin{bmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,m}\\ a_{2,1} & a_{2,2} & \cdots & a_{2,m}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n,1} & a_{n,2} & cdots & a_{n,m}\end{bmatrix}\cdot\begin{bmatrix} b_{1,1} & b_{1,2} & \cdots & b_{1,p}\\ b_{2,1} & b_{2,2} & \cdots & b_{2,p}\\ \vdots & \vdots & \ddots & \vdots\\ b_{m,1} & b_{m,2} & cdots & b_{m,p} \end{bmatrix}=\begin{bmatrix} \sum_{i=1}^{m}a_{1,i}\cdot b_{i,1} & sum_{i=1}^{m}a_{1,i}\cdot b_{i,2} & \cdots & \sum_{i=1}^{m}a_{1,i}\cdot b_{i,p}\\ \sum_{i=1}^{m}a_{2,i}\cdot b_{i,1} & \sum_{i=1}^{m}a_{2,i}\cdot b_{i,2} & \cdots & \sum_{i=1}^{m}a_{2,i}\cdot b_{i,p}\\ \vdots & \vdots & \ddots & \vdots\\ \sum_{i=1}^{m}a_{n,i}\cdot b_{i,1} & \sum_{i=1}^{m}a_{n,i}\cdot b_{i,2} & \cdots & \sum_{i=1}^{m}a_{n,i}\cdot b_{i,p}\end{bmatrix}
gdzie:
- m, n, p ∈ N{0}
Pewnym zaskoczeniem może się wydawać fakt, że iloczyn macierzy A, B jest nieprzemienne, czyli A⋅B≠B⋅A.
Przykłady
Obliczyć iloczyn macierzy A⋅B, B⋅A oraz C⋅D.
Dane:
Rozwiązanie:
Iloczyn A⋅B:
Iloczyn B⋅A:
Iloczyn macierzy kwadratowych C⋅D:
