Całkowanie numeryczne - metoda prostokątów

Autor podstrony: Krzysztof Zajączkowski

Stronę tą wyświetlono już: 11580 razy

Całkowanie numeryczne metodą prostokątów należy do jednych z najprostszych sposobów numerycznego obliczania przybliżonej wartości całki oznaczonej z danej funkcji f(x) w przedziale od a do b. Metoda ta polega na podzieleniu tegoż przedziału na elementarne prostokąty o wymiarach 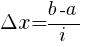Delta x = {{b - a} / {i}} na f(x_i), gdzie i jest indeksem kolejnego prostokąta należącego na pewnego przedziału.

Graficzny opis metody obliczania pola powierzchni zawartej pomiędzy funkcją <b>f(x)</b> a osią <b>x</b> w przedziale <<b>a</b>,<b>b</b>>. — Rys. 1
Graficzny opis metody obliczania pola powierzchni zawartej pomiędzy funkcją **f(x)** a osią x w przedziale <a,b> numeryczną metodą prostokątów.

W językach programowania takich jak C++ do wykorzystania tego algorytmu konieczne jest zaimplementowanie algorytmu ONP, który powstał jako modyfikacja algorytmu notacji polskiej Jana Łukasiewicza. W przypadku języków skryptowych takich jak PHP czy Python można posłużyć się funkcją eval, której użycie ze względów bezpieczeństwa jest niewskazane.

Oto przykład prostego programu obliczającego tą metodą całkę podanej na wejście funkcji napisany w Pythonie:

#!/usr/bin/env python def integrate(function, a, b, i): dx = (b - a) / i integr = 0 for x in range(i): x = x * dx + a integr += dx * eval(function) return integr def main(args): function = input("Funkcja: ") a = float(input("Początek przedziału: ")) b = float(input("Koniec przedziału: ")) i = int(input("Liczba podprzedziałów")) print("Całka z funkcji {funkcjon} po przedziale od {a} do {b} = {integrate}".format(funkcjon = function, a = a, b = b, integrate = integrate(function, a, b, i))) return 0 if __name__ == '__main__': import sys sys.exit(main(sys.argv))

Przykład działania dla f(x) = x₂, a = 0, b = 1, oraz i = 10:

Funkcja: x**2
Początek przedziału: 0
Koniec przedziału: 1
Liczba podprzedziałów10
Całka z funkcji x**2 po przedziale od 0.0 do 1.0 = 0.2850000000000001
Aby kontynuować, naciśnij dowolny klawisz . . .

Jak widać, dla i = 10 dokładność jest kiepska, zważywszy na fakt, że:

[1]

Zapis wyrażenia w formacie TeX-a:

\int_{0}^{1}{x^2}=\frac{1}{3}

Nieco lepsze wyniki można uzyskać dla i = 100:

Funkcja: x**2
Początek przedziału: 0
Koniec przedziału: 1
Liczba podprzedziałów100
Całka z funkcji x**2 po przedziale od 0.0 do 1.0 = 0.32835000000000014
Aby kontynuować, naciśnij dowolny klawisz . . .