Numeryczne obliczanie pochodnej funkcji w danym punkcie

Autor podstrony: Krzysztof Zajączkowski

Stronę tą wyświetlono już: 25595 razy

Numeryczne obliczanie pochodnej funkcji f(x) w danym punkcie x sprowadza się do zastosowania ogólnej graficznej interpretacji przybliżonej wartości pochodnej, która pokazana została na poniższym rysunku. Widać tutaj dwa punkty P₁ i P₂, które są oddalone od siebie o wartość Δx, współrzędne y-kowe tych punktów są dane funkcją f(x) dla punktu pierwszego i f(x + Δx) dla punktu drugiego. Punty P₁ i P₂ wyznaczają pewną prostą, której kąt β przy bardzo małym Δx w przybliżeniu jest równy kątowi stycznej do punktu P₁.

Rys. 1
Obliczanie przybliżonej wartości pochodnej - graficzna interpretacja.

Wiedząc, że pochodna funkcji w danym jej punkcie jest równa tangensowi kąta nachylenia prostej stycznej do tej funkcji można obliczyć numerycznie pierwszą pochodną funkcji f(x) korzystając z następującego wzoru:

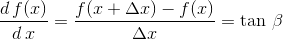Wzór na pierwszą pochodną całki numerycznej w zadanym punkcie x

[1]

Zapis wyrażenia w formacie TeX-a:

\frac{d\,f(x)}{d\,x}=\frac{f(x + \Delta x) - f(x)}{\Delta x}=\tan\, \beta

Korzystając z wzoru [1] można wyznaczyć wzór na przybliżoną wartość drugiej pochodnej funkcji:

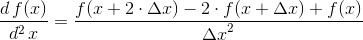[2]

Zapis wyrażenia w formacie TeX-a:

\frac{d\,f(x)}{d^2\,x}=\frac{f(x + 2\cdot\Delta x) - 2 \cdot f(x + \Delta x) + f(x)}{{\Delta x}^2}

W językach programowania takich jak C++ do wykorzystania tego algorytmu konieczne jest zaimplementowanie algorytmu ONP, który powstał jako modyfikacja algorytmu notacji polskiej Jana Łukasiewicza. W przypadku języków skryptowych takich jak PHP czy Python można posłużyć się funkcją eval, której użycie ze względów bezpieczeństwa jest niekiedy niewskazane.

Oto przykład prostego programu napisanego w Pythonie obliczającego tą metodą pierwszą i drugą pochodną podanej na wejście funkcji:

#!/usr/bin/env python from math import * def diff(function, x, dx): f_x1 = eval(function) x += dx f_x2 = eval(function) return (f_x2 - f_x1) / dx def diff2(function, x, dx): f_x1 = eval(function) x += dx f_x2 = eval(function) x += dx f_x3 = eval(function) return (f_x3 - 2 * f_x2 + f_x1) / (dx * dx) def main(args): function = input("Podaj funkcję f(x): ") x = float(input("Punkt dla pochodnej funkcji f(x): ")) dx = float(input("Rozmiar elementarnego przesunięcia: ")) print("Pochodna funkcji {function} w punkcie {x} dla dx = {dx} jest równa: {diff}".format(function = function, x = x, dx = dx, diff = diff(function, x, dx))) print("Druga pochodna funkcji {function} w punkcie {x} dla dx = {dx} jest równa: {diff2}".format(function = function, x = x, dx = dx, diff2 = diff2(function, x, dx))) return 0 if __name__ == '__main__': import sys sys.exit(main(sys.argv))

Przykład obliczenia pierwszej i drugiej pochodnej funkcji f(x) = sin(x) dla x = 1 i Δx = 0.1:

Podaj funkcję f(x): sin(x)
Punkt dla pochodnej funkcji f(x): 1
Rozmiar elementarnego przesunięcia: 0.1
Pochodna funkcji sin(x) w punkcie 1.0 dla dx = 0.1 jest równa: 0.4973637525353891
Druga pochodna funkcji sin(x) w punkcie 1.0 dla dx = 0.1 jest równa: -0.8904649347747926
Aby kontynuować, naciśnij dowolny klawisz . . .

Pierwsza pochodna funkcji f(x) = sin(x) jest równa f'(x) = cos(x) a więc wartość tej funkcji dla x = 1 [rad] wynosi f'(1) = 0.540302305, natomiast druga pochodna to f''(x) = -sin(x), dla której wartość tej funkcji dla x = 1 [rad] wynosi f''(x) = -0.841470984. Różnice dla Δx = 0.1 są znaczące, więc warto zmniejszyć ten parametr do np. Δx = 0.00001 w wyniku czego otrzymany zostanie następujący rezultat:

Podaj funkcję f(x): sin(x)
Punkt dla pochodnej funkcji f(x): 1
Rozmiar elementarnego przesunięcia: 0.00001
Pochodna funkcji sin(x) w punkcie 1.0 dla dx = 1e-05 jest równa: 0.5402980985058647
Druga pochodna funkcji sin(x) w punkcie 1.0 dla dx = 1e-05 jest równa: -0.8414757779462433
Aby kontynuować, naciśnij dowolny klawisz . . .

Jak widać rozbieżności są znacznie mniejsze niż poprzednio.