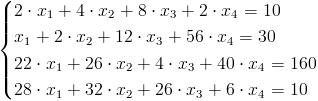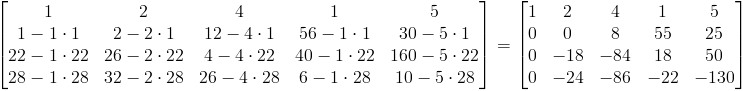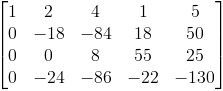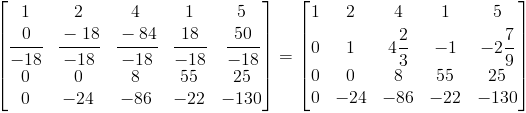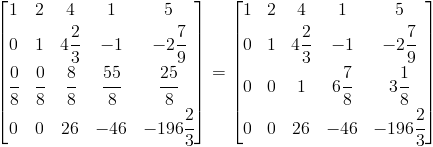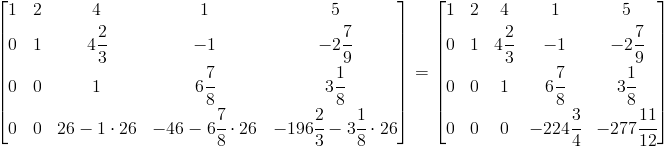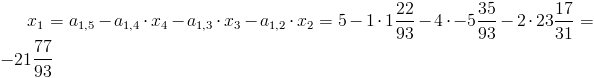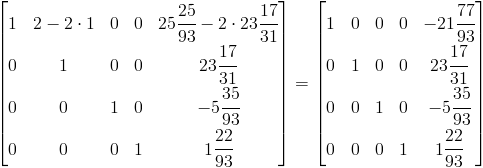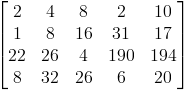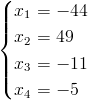Rozwiązywanie układów równań metodą eliminacji Gaussa
Stronę tą wyświetlono już: 13724 razy
Rozwiązywanie układów równań liniowych możliwe jest poprzez zastosowanie metody eliminacji Gaussa. Metoda ta sprowadza macierz danego układu równań do macierzy jednostkowej lub macierzy trójkątnej z jednoczesnym wyznaczeniem wartości niewiadomych x1, x2, ... , xn.
Z współczynników stojących przy niewiadomych oraz wyrazów wolnych należy utworzyć macierz:
gdzie:
- a1,1, ... , an,n - odpowiadają współczynnikom stojącym przy niewiadomych x1, x2, ... , xn;
- a1, n+1, a2, n+1, ... , an,n+1 - odpowiadają wyrazom wolnym z układu równań [1].
Przekształcenie powyższej macierzy do macierzy trójkątnej górnej odbywa się etapowo w dwóch krokach, które realizowane są dla wartości i zmieniającej się od 1 do n:
- Podzielić i-ty wiersz macierzy przez odwrotność jej argumentu ai,i w następujący sposób:
Przykład dla i=1:
-
Dla każdego wiersza o indeksie k takim że i<k≤n odjąć otrzymany wiersz Wi' przemnożony przez argument ai,k:
Przykład dla k= 2, ... , n:
Aby zredukować do zera argumenty macierzy znajdujące się nad przekątną główną należy operację odejmowania przeprowadzić dla k∈{1, 2, ..., n}{i}.
Macierz powstała w wyniku jednokrotnego wykonania kroków 1, 2 stanowi dane wejściowe dla następnego cyklu. W początkowej fazie, dla i=1 dane wejściowe stanowi macierz [2].
Po przeprowadzeniu wszystkich etapów dla i=1, 2, ... , n otrzymana zostanie następująca macierz trójkątna górna:
gdzie:
- bi,j - argumenty macierzy otrzymane po przeprowadzeniu metody eliminacji Gaussa na macierzy [2]
Wartość niewiadomej xn układu równań [1] po przeprowadzeniu metody eliminacji Gaussa jest równa:
natomiast kolejne niewiadome o indeksach i=n-1, n-2, ... , 1 obliczyć można za pomocą następującego wzoru:
Przykład
Rozwiązać metodą eliminacji Gaussa do postaci macierzy trójkątnej górnej następujący układ równań:
Zacząć należy od utworzenia macierzy:
Etap pierwszy dla i = 1
Krok pierwszy - podzielenie pierwszego wiersza przez a1,1
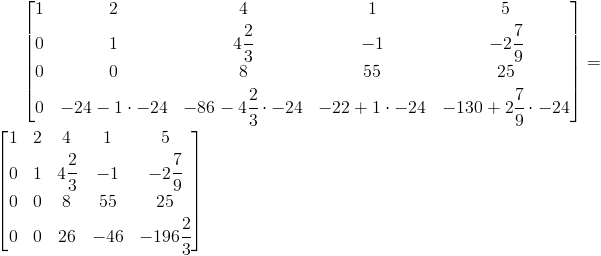
Krok drugi - odjęcie od wierszy 2, 3, 4 wiersza pierwszego pomnożonego odpowiednio przez współczynniki a2,1, a3,1, a4,1.
Ponieważ argument a2,2 uzyskanej macierzy jest równy 0, konieczna jest zamiana miejscami wiersza drugiego z trzecim w następujący sposób:
Etap drugi dla i=2
Krok pierwszy - podzielenie drugiego wiersza przez a2,2
Krok drugi - odjęcie od wierszy 3, 4 wiersza drugiego pomnożonego odpowiednio przez współczynniki a3,2, a4,2, jednakże wiersz trzeci można pominąć, ponieważ argument a3,2=0.
Etap trzeci dla i=3
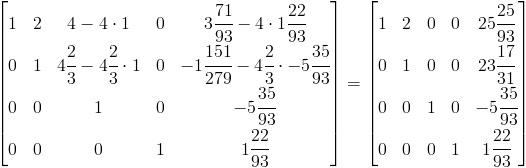
Krok pierwszy - podzielenie wiersza trzeciego przez argument a3,3
Krok drugi - odjęcie od wiesza czwartego wiersza trzeciego pomnożonego przez współczynnik a4,3.
Etap czwarty dla i=4
Krok pierwszy - podzielenie wiersza czwartego przez argument a4,4
Kroku drugiego nie ma i nie będzie, ponieważ brak jest wierszy do przeliczenia.
Według wzoru [6] niewiadoma x4 jest równa:
Pozostałe niewiadome można obliczyć według wzoru [7].
Można zredukować do zera argumenty macierzy znajdujące nad przekątną główną macierzy uzyskanej w kroku czwartym za pomocą trzech etapów otrzymując w ten sposób w ostatniej kolumnie wartości niewiadomych x1, x2, x3, x4.
Etat pierwszy - od wierszy 1, 2, 3 odjąć wiersz czwarty pomnożony odpowiednio przez współczynniki a1,4, a2,4, a3,4.
Etap drugi - od wierszy 1, 2 odjąć wiersz trzeci pomnożony odpowiednio przez współczynniki a1,3, a2,3.
Etap trzeci - od wiersza pierwszego odjąć wiersz drugi pomnożony przez współczynnik a1,2.
Ponieważ swego czasu zrobiłem program, który w przebiegły sposób wykorzystuje metodą eliminacji Gausa do rozwiązywania liniowych układów równań, więc użyję go tutaj do rozwiązania tego samego układu równań podając mu na wejście następujące dane:
by program po chwili wypluł na powierzchnię ekranu następujący wynik:
Jak widać powyżej, program nie tylko rozwiązuje ale i rozpisuje kolejne etapy.
Przykład do samodzielnego rozwiązania:
Odpowiedź:

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_1155.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_1202.gif)
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_1203.gif)

![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_1204.gif)
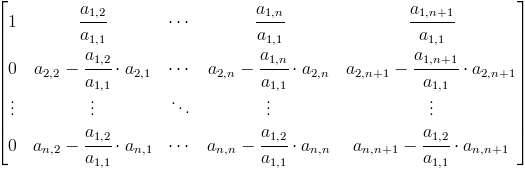
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_1207.gif)
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_1208.gif)
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_1209.gif)