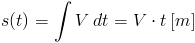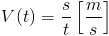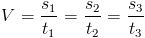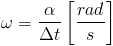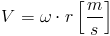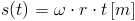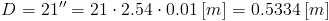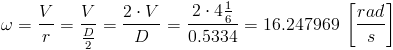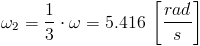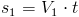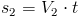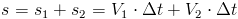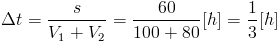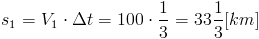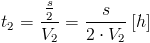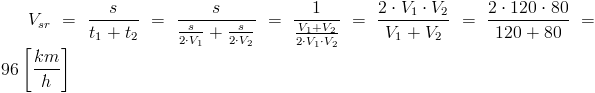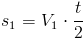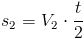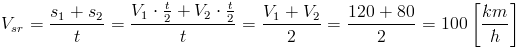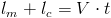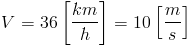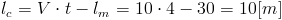Ruch jednostajny
Stronę tą wyświetlono już: 7487 razy
Ruch jednostajny w którym prędkość jest stała V=const (const ang. stała). Drogę s przebytą przez ciało poruszające się ruchem jednostajnym określa poniższy wzór:
Oczywiście zależność prędkości od czasu i przebytej drogi w ruchu jednostajnym można uzyskać przekształcając wzór [1] do następującej postaci:
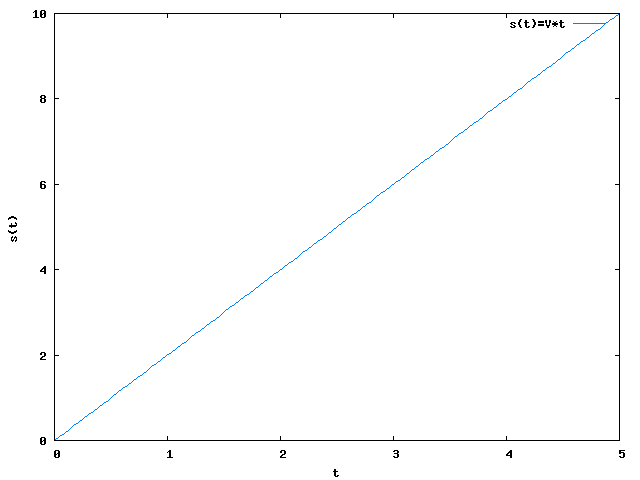
Funkcja s(t) dla ruchu jednostajnego jest funkcją liniową, co wynika z rysunku 1.
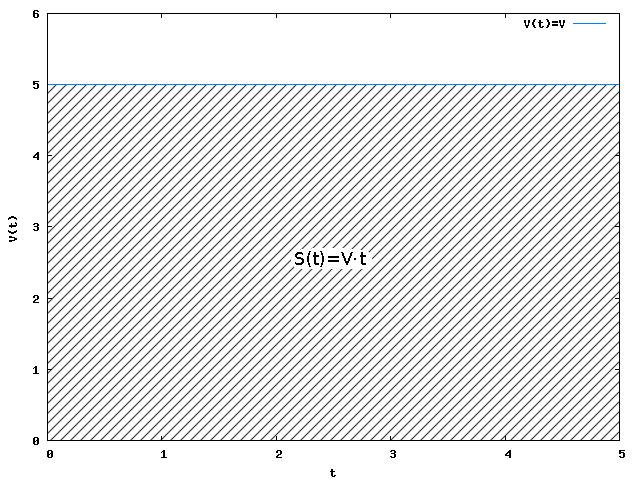
Pole powierzchni zawartej pod wykresem funkcji V(t) dla ruchu jednostajnego jest równe polu powierzchni prostokąta, którego boki mają wymiary V(t)×t jak na rysunku 2.
W ruchu jednostajnym stosunek przemieszczenia do jednostki czasu, w której owo przemieszczenie zostało zrealizowane musi być stałe, albowiem w przeciwnym przypadku mamy do czynienia z ruchem nie jednostajnym. Innymi słowy, jeżeli dla zadanych przedziałów czasów t1, t2, t3 znane są wartości przebytej w owym czasie drogi s1, s2, s3 to jeżeli spełniona jest następująca równość:
wtedy to prędkość V poruszającego się obiektu jest stała.
Szczególnym rodzajem ruchu jednostajnego jest ruch po linii prostej oraz ruch po okręgu. Pierwszy rodzaj ruchu jest ważny przez wzgląd na I zasadę dynamiki Newtona, jednakże nie będę się tutaj rozpisywał o tym ze względu na fakt, że temat ten dotyczy dynamiki a nie kinematyki. W przypadku drugiego rodzaju ruchu konieczne jest jego zapisanie w postaci prędkości kątowej ω, której wartość jest równa stosunkowi kąta α wyrażonego najczęściej w radianach do przedziału czasu Δt, w którym owe przemieszczenie kątowe nastąpiło. Wzór na jednostajną prędkość kątową obiektu jest więc następujący:
Możliwe jest obliczenie liniowej prędkości obwodowej obiektu poruszającego się po okręgu jednakże w tym celu konieczna jest znajomość promienia r, po którym ów obiekt się obraca. Prędkość obwodowa jest więc dana następującą zależnością:
Droga przebyta przez ciało poruszające się ruchem jednostajnym po okręgu może zostać obliczona poprzez podstawienie do wzoru [1] za V wartości z wzoru [4] otrzymując tym samym następujący wzór:
Zadania
1 W ciągu godziny Gienek przejechał 15 kilometrów. Obliczyć prędkość z jaką poruszał się Gienek jeżeli wiadomo że jego ruch był jednostajny.
Rozwiązanie:
Należy zastosować wzór [2] w celu obliczenia prędkości.
2 Obliczyć prędkość kątową ω kół roweru Gienka bazując na obliczeniach wykonanych w zadaniu 1 oraz wiedząc, że średnica kół roweru Gienka jest równa 21 cali.
Rozwiązanie:
Koniecznie należy przeliczyć cale na metry:
Przekształcając wzór [4] można obliczyć prędkość kątową ω, należy jednak pamiętać że w wzorze występuje promień r który z kolei jest równy połowie danej w zadaniu średnicy koła roweru D.
3 Obliczyć prędkość kątową ωp pedałów roweru Gienka bazując na danych z zadania 2 i wiedząc że stosunek przełożenia prędkości z zębatki sprzężonej z pedałami roweru do zębatki sprzężonej z tylnym kołem jest równe 1:3 co oznacza że na jeden pełny obrót pedałami roweru przypadają trzy obroty tylnego koła.
Rozwiązanie:
Prędkość kątowa pedałów roweru jest równa jednej trzeciej prędkości kątowej koła tylnego, a więc:
4 Z Zadupia Małego do Zadupia Dużego wyjeżdża pociąg pośpieszny z stałą prędkością V1=100[km/h] w tym samym czasie z Zadupia Dużego do Zadupia Małego wyrusza pociąg osobowy z stałą prędkością V2=80[km/h]. Ponieważ ktoś zrobił rozkład jazdy po pijaku i nasze pociągi jadą teraz jednym torem w związku z czym dojdzie do kolizji. Oblicz: w jakiej odległości od Zadupia Małego dojdzie do kolizji pociągów oraz określ przedział czasu od momentu wyruszenia pociągów ze stacji kolejowych do momentu ich kolizji. Odcinek trasy łączący Zadupie Małe i Zadupie Duże sfinansowany ze środków Unii Jełopejskiej liczy sobie 60[km].
W zadaniu należy pominąć czas potrzebny na rozpędzenie pociągów.
Rozwiązanie:
Zdaję sobie sprawę, że są ludzie którym tego typu zadania spędzają sen z powiek jednakże nie takie zadanie straszne jak uczniowie mówią. Droga s1 jaką przebędzie pociąg wyruszający z Zadupia Małego jest równa:
zaś droga s2 przebyta przez pociąg wyruszający z Zadupia Dużego:
oczywistym jest fakt, że suma s1+s2 musi być równa długości trasy łączącej nasze miejscowości. Tak więc można napisać następującą równość:
przekształcając powyższe równanie otrzymuje się wzór na przedział czasu Δt, po którym nastąpi kolizja pociągów:
Pozostało jedynie obliczenie w jakiej odległości od Zadupia Małego dojdzie do kolizji, ale na to jest już wzór:
5 Gienek pojechał samochodem z rodziną nad jezioro, połowę trasy przebył z prędkością V1=120[km/h] zaś drugą połowę z prędkością V2=80[km/h]. Obliczyć średnią prędkość, z jaką Gienek jechał.
Rozwiązanie:
Najsamprzód określić trzeba czas przejazdu dla prędkości V1:
oraz dla prędkości V2:
Prędkość średnia Vśr jest więc równa:
6 W drodze powrotnej znad jeziora Gienek połowę czasu przejechał z prędkością V1=80[km/h] zaś drugą połowę czasu z prędkością V2=120[km/h]. Obliczyć średnią prędkość z jaką Gienek wracał do domu.
Rozwiązanie:
Zacząć należy od określenia drogi s1 przebytej z prędkością V1 w następujący sposób:
oraz z prędkością V2:
Prędkość średnią można obliczyć w następujący sposób:
7 Równoległymi torami jadą dwa pociągi: pierwszy z prędkością V1=70[km/h] oraz drugi z prędkością V2=100[km/h]. Obliczyć prędkość pociągu drugiego względem pierwszego.
Rozwiązanie:
Pociąg pierwszy porusza się względem drugiego z prędkością równą V2-V1=30[km/h]..
8 Przez trzydziesto metrowej długości most przejeżdża ciężarówka z prędkością V=36[km/h]. Obliczyć jej długość wiedząc że od momentu gdy przód ciężarówki zrównał się z początkiem mostu do chwili gdy koniec ciężarówki zrównał się z końcem mostu upłynęły 4[s].
Rozwiązanie:
Dystans jaki pokonała ciężarówka jest równy sumie długości mostu lm oraz ciężarówki lc. Znając prędkość i czas można tą samą odległość wyznaczyć za pomocą wzoru [1], w związku z czym prawdziwa jest równość:
Prędkość V należy wyrazić w metrach na sekundę:
Przekształcając wcześniejsze równanie uzyskuje się wzór na długość ciężarówki: