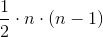Stronę tą wyświetlono już: 4744 razy
Algorytm sortowania przez wstawienie w odróżnieniu od sortowania bombelkowego w kolejnych przejściach p sprawdza k-ty element tablicy z elementami o indeksach i < k i gdy i-ty element > k-ty to następuje przeniesienie elementu k-tego za element i-ty chyba, że żaden element nie okaże się mniejszy od k-tego wtedy tenże element ląduje na samym początku tablicy. Przejścia są powtarzane aż do p = n - 1, gdzie n - to liczba elementów sortowanej tablicy.
- czerwony - element tablicy, który jest mniejszy od sortowanego elementu;
- niebieski - element tablicy, który jest większy od sortowanego elementu;
- pomarańczowy - element tablicy, który jest w danym przejściu sortowany;
- zielony - pozostałe elementy tablicy
W najgorszym przypadku liczba kroków niezbędnych do wykonania w implementacji z powyższej animacji wynosi:
Warto też nadmienić, że sortownie przez wstawianie jest szybsze od sortowania bombelkowego dla danych losowych. Dzieje się tak dlatego, że liczba wykonywanych operacji zamiany miejscami sortowanych wartości jest znacznie mniejsza niż w przypadku sortowania bombelkowego. Nie zmienia to niemniej faktu, że sortowanie bombelkowe, gdy dane są częściowo posortowane może się okazać znacznie szybsze od sortowania przez wstawienie.