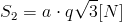Reakcje belek statycznie wyznaczalnych
Stronę tą wyświetlono już: 91165 razy
Czas zacząć w końcu zabawę w obliczanie reakcji belek statycznie wyznaczalnych, zanim jednak to nastąpi konieczne jest zapoznanie się z kwestiami dotyczącymi umownych oznaczeń rysunkowych występujących w zadaniach tego typu.
Oznaczenia i typy podpór belek
Podpory o jednej niewiadomej
| Podparcie na idealnie gładkiej powierzchni, jeżeli na rysunku zadania nie ma oznaczeń reakcji to w treści zadania powinno być zaznaczone z jakim typem powierzchni styka się krawędź belki. Reakcja tego typu podpór często jest nazywana naciskiem. Brak reakcji dodatkowej spowodowany jest brakiem tarcia lub (w przypadku układów rzeczywistych) pomijalnie małym tarciem | |
| Podparcie na podporze z łożyskiem, która morze przenosić tylko obciążenia prostopadłe do jej powierzchni. W praktyce jest to odpowiednik z poprzedniego typu podpory. | |
| Cięgno, zamocowane jednym końcem np. do ściany a drugim do belki. Tego typu układ również ma reakcję, która znajduje się w cięgnie. | |
| Tego typu podparcie umożliwia przesuwanie się belki po ostrzu w przypadkach, gdy równowaga sił nie jest zachowana. Warto zauważyć, że reakcja przy tego typu podporach jest zawsze prostopadła do płaszczyzny belki a nie podpory (ostrza). |
Podpory o dwóch niewiadomych
| Podparcie na powierzchni chropowatej, jeżeli na rysunku zadania nie ma oznaczeń reakcji to w treści zadania powinno być zaznaczone z jakim typem powierzchni styka się krawędź belki. Reakcje tego typu podpór często są nazywane naciskiem (prostopadła do płaszczyzny) oraz tarciem (równoległa do płaszczyzny). Tarcie może być pominięte, gdy jest pomijalnie małe (co nie ma miejsca na powierzchniach chropowatych). | |
| Tego typu podparcie uniemożliwia przemieszczanie się belki w dwóch osiach. |
Podpory o trzech niewiadomych
| Utwierdzenie sztywne przenosi oprócz reakcji moment obrotowy, spowodowany działaniem sił zewnętrznych. |
Oznaczenia podstawowych typów oddziaływań
Oznaczenie obciążenia ciągłego
| Obciążenie ciągłe wyrażone w niutonach na metr długości (np. belki). | |
| Możliwe jest wyznaczenie wektora siły wypadkowej poprzez przemnożenie wartości obciążenia ciągłego przez odległość, na której się to obciążenie rozkłada. Punkt zaczepienia wektora tej siły znajduje się w środku ciężkości obciążenia ciągłego, czyli w połowie długości na którą się ono rozkłada. |
Oznaczenie siły
| Wektor siły. W przypadku wyznaczania momentu obrotowego (momentu siły) należy przemnożyć jego wartość razy promień działania siły względem obranego punktu, gdzie promieniem jest długość odcinka poprowadzonego prostopadle do linii wektora siły z obranego punktu. |
Oznaczenie momentu zginającego (momentu siły)
| Moment siły (znaki: dodatni - gdy moment działa przeciwnie do kierunku wskazówek zegara, ujemny - w przeciwnym przypadku). | |
| Para sił - czyli to samo co powyżej (znaki: dodatni - gdy moment działa przeciwnie do kierunku wskazówek zegara, ujemny - w przeciwnym przypadku). |
Warunki statycznej wyznaczalności
Belki statycznie wyznaczalne muszą mieć odebrane wszystkie stopnie swobody (ruch wzdłuż osi x i y oraz obrót), ponieważ układ nie odbierający trzech stopni swobody nie jest układem statycznie wyznaczalnym a jedynie mechanizmem, który może się przemieszczać pod wpływem działających sił. Oznacza to w praktyce, że belka musi być podparta tak aby występowały trzy reakcje. W układach trójwymiarowych liczba reakcji niezbędnych do utrzymania obiektu w bezruchu musi być odpowiednio większa.
Zadanie 1
Dana jest belka podparta na podporze stałej i przesuwnej jak na rysunku 1.
Dane:
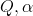
Wyznaczyć:
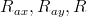
Rozwiązanie:
Dla osi X wystarczy napisać jedno następujące statyczne równanie równowagi:
Z równania [1] można wyliczyć składową X reakcji podpory stałej:
Nieco gorzej sprawa ma się w przypadku reakcji wypadkowej y podpory stałej i reakcji podpory przesuwnej. Tutaj można postąpić w dwojaki sposób:
Ułożyć równanie sumy momentów zginających względem punktu zaczepienia podpory stałej oraz równanie drugie sumy momentów zginających względem punktu zaczepienia podpory przesuwnej.
Ułożyć równanie sumy sił wypadkowych i reakcji wypadkowych dla osi y oraz momentu obrotowego najlepiej względem punktu zaczepienia jednej z podpór.
Czasami nieco łatwiej jest zastosować metodę pierwszą, ponieważ umożliwia ona niekiedy wyznaczenie reakcji bez podstawiania z jednego równania do drugiego.
Tak więc równania dla przypadku pierwszego mają następującą postać:
Powyższe równanie zostało mocno rozwinięte, a wszystko po to aby było widać, dlaczego w równaniu tym można pominąć reakcje podpory stałej oraz składową x siły Q. W przyszłości nie równania tego typu nie będą już tak przesadnie rozpisywane.
Z równania [2] można a nawet trzeba wyznaczyć składową Y reakcji podpory przesuwnej otrzymując następującą wartość:
Równanie drugie:
No i zostało jedynie wyznaczenie z równania [3] składowej y reakcji podpory stałej:
Zadanie do samodzielnego rozwiązania: Oblicz reakcje y-kowe podpór wykorzystując drugi sposób wyznaczania tych reakcji reakcji.
Zadanie 2 - do samodzielnego rozwiązania
Wyznaczyć reakcje podpór belki statycznie wyznaczalnej z rysunku 2.
Tym razem bez żadnych odpowiedzi, przecie to jest prostsze niż odebranie dzieciakowi lizaka.
Zadanie 3
Obliczyć reakcje belki statycznie wyznaczalnej z rysunku 3.
Dane:
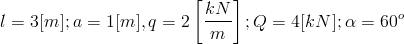
Rozwiązanie:
Jak wcześniej była już o tym mowa, obciążenie ciągłe można (a nawet należy) zastąpić siłą wypadkową umieszczoną w środku ciężkości tego obciążenia. Obliczenie wartości siły działającej na belkę wymaga przemnożenia wartości obciążenia przez długość na której się ono rozkłada.
Najpierw należy napisać równanie równowagi dla osi x:
Dla odmiany kolejne reakcje wyznaczone zostaną za pomocą sumy wypadkowych na oś Y i sumy momentów gnących względem punktu zaczepienia podpory stałej. A oto i pierwsze równanie:
Jak widać z równania [5] nic nie da się wyznaczyć, trzeba napisać jeszcze jedno równanie:
Pozostało jedynie wyznaczyć składową y reakcji podpory stałej poprzez przekształcenie równania [5] i podstawienie do niego wartości wyliczonej z równania [6]:
Można jeszcze pokusić się o wyznaczenie wartości reakcji wypadkowej podpory stałej w następujący sposób:
A skoro reakcja podpory stałej wyliczona została, to i kąt jej położenia względem osi x w następujący sposób obliczyć można:
Zadanie 4
Obliczyć reakcje podpór belki z rysunku 4.
Dane:
![q [N/m]; alfa=30 stopni; L [m]](rownania/w_029.gif)
Rozwiązanie:
Najpierw równanie równowagi dla sumy momentów gnących względem punktu zaczepienia podpory stałej:
Teraz równanie równowagi dla sumy momentów gnących względem punktu zaczepienia podpory przesuwnej:
Pozostało już tylko napisać równanie równowagi dla sumy rzutów sił na oś X:
Małe zadanie na zakończenie: Wyznacz, tak jak już wcześniej było to robione w zadaniu 1, reakcję wypadkową podpory stałej i kąt jej pochylenia względem osi x.
Zadanie 5
Wyznaczyć reakcje utwierdzenia sztywnego belki pokazanej na rysunku 5.
Dane:
![q[N/m]; a[m]; alfa=30 stopni; Q=2 * q * a [N]; M=3 * q * a ^ 2 [Nm]](rownania/w_033.gif)
Rozwiązanie:
Najpierw rozprawię się z momentem utwierdzenia Mau układając równanie równowagi dla momentów gnących względem punktu utwierdzenia sztywnego:
Teraz kolej na reakcję Rax:
Pozostało jedynie rozprawić się z reakcją Ray:
Zadanie domowe: Wyznaczyć wypadkową reakcję utwierdzenia sztywnego i jej kąt nachylenia względem osi x.
Odpowiedź:
Zadanie 6 - do samodzielnego rozwiązania
Wyznaczyć reakcje podpory stałej i przesuwnej dla belki z rysunku 6.
Dane:
![l=3[m]; a=2 [m]; q=2[kN/m]; alfa=30 stopni; M=3[kNm]](rownania/w_039.gif)
Odpowiedź:
Zadanie 7
Obliczyć reakcje podpory przesuwnej i cięgien belki z rysunku 7.
Dane:
![a[m]; alfa=30 stopni; beta=60 stopni; q[N/m]; M=2*q*a^2[Nm]](rownania/w_045.gif)
Rozwiązanie:
Najpierw wyznaczona zostanie reakcja R z układu równowagi sumy momentów gnących względem punktu zaczepienia cięgien z belką:
No to teraz równanie dla sumy rzutów sił na oś x:
I pozostało już tylko równanie sum momentów skręcających względem punktu zaczepienia podpory przesuwnej:
Teraz już można wyliczyć siłę w pręcie drugim:

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_016.gif)
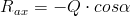
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_018.gif)
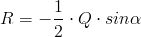
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_020.gif)
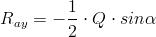
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_023.gif)
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_024.gif)
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_025.gif)
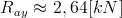
![Równanie [7]](https://obliczeniowo.com.pl/rownania/w_027.gif)
![Równanie [8]](https://obliczeniowo.com.pl/rownania/w_028.gif)
![Równanie [9]](https://obliczeniowo.com.pl/rownania/w_030.gif)
![Równanie [10]](https://obliczeniowo.com.pl/rownania/w_031.gif)
![Równanie [11]](https://obliczeniowo.com.pl/rownania/w_032.gif)
![Równanie [12]](https://obliczeniowo.com.pl/rownania/w_034.gif)
![Równanie [13]](https://obliczeniowo.com.pl/rownania/w_035.gif)
![Równanie [14]](https://obliczeniowo.com.pl/rownania/w_036.gif)
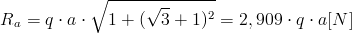
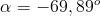
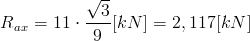
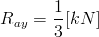

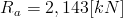

![Równanie [15]](https://obliczeniowo.com.pl/rownania/w_046.gif)
![Równanie [16]](https://obliczeniowo.com.pl/rownania/w_047.gif)
![Równanie [17]](https://obliczeniowo.com.pl/rownania/w_048.gif)