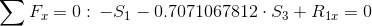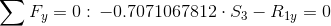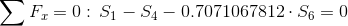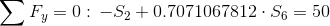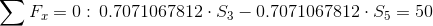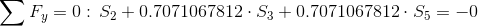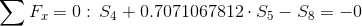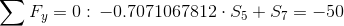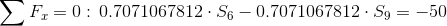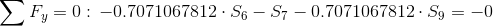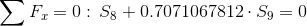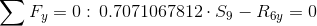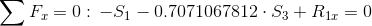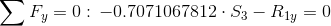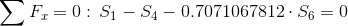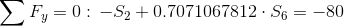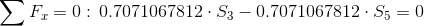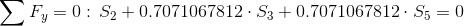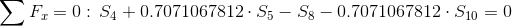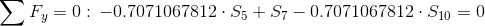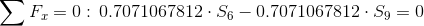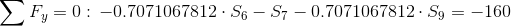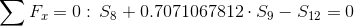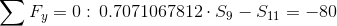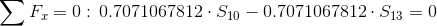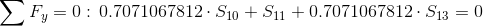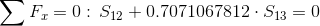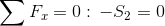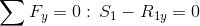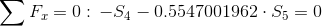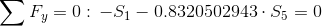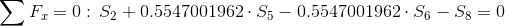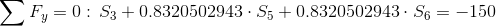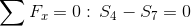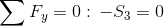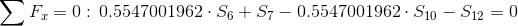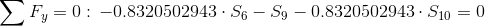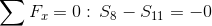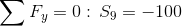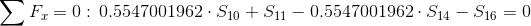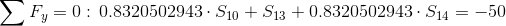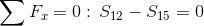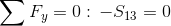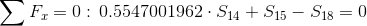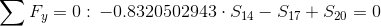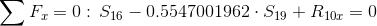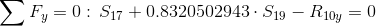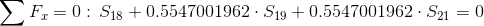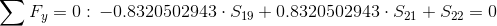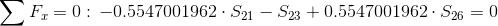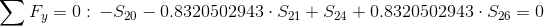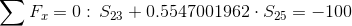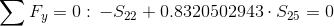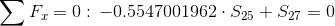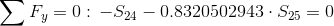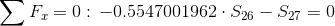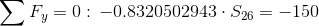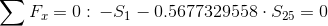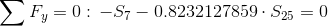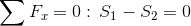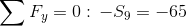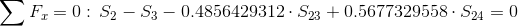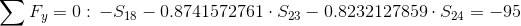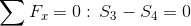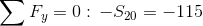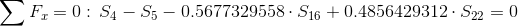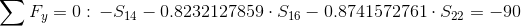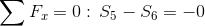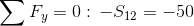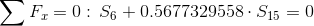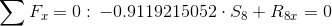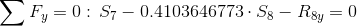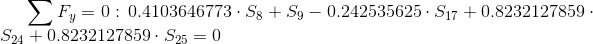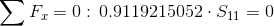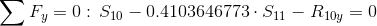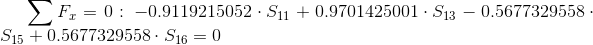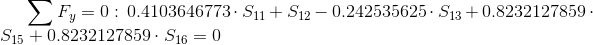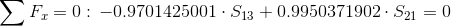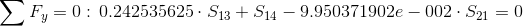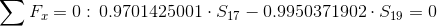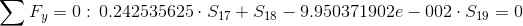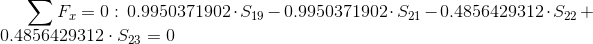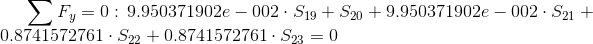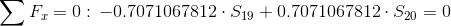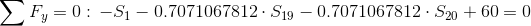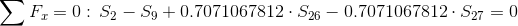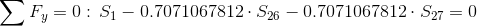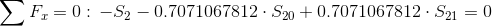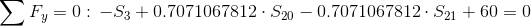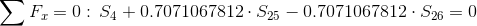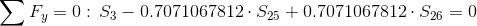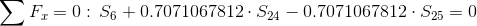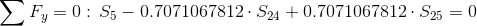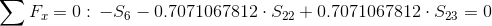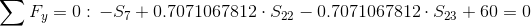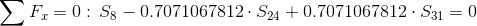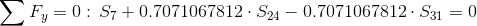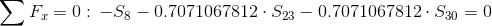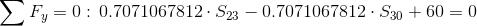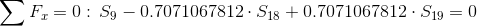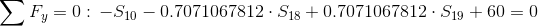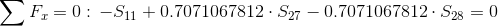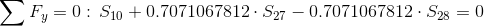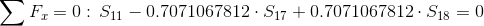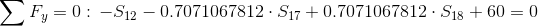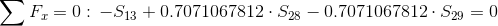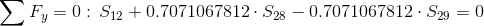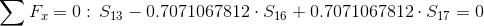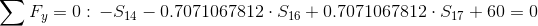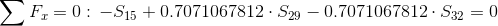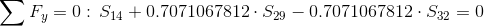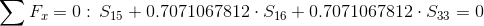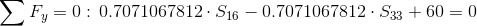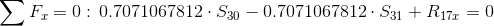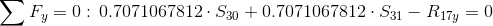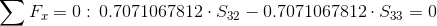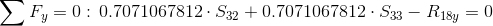Kratownice statycznie wyznaczalne
Stronę tą wyświetlono już: 44846 razy
Podstawowe definicje:Kratownica - układ nieważkich prętów połączonych węzłami, który może być obciążony jedynie siłami skupionymi w jej węzłach. Kratownice można podzielić na płaskie i przestrzenne.
Węzeł - punkt, w którym pręty kratownicy łączą się.
Pręt - element leżący pomiędzy dwoma węzłami kratownicy.
Kratownica płaska jest statycznie wyznaczalna, gdy jest możliwe wyznaczenie jej reakcji za pomocą równań równowagi, oraz gdy podwojona liczba węzłów w kratownicy jest równa sumie liczby prętów p oraz reakcji r kratownicy. Wynika to z faktu, że dla każdego węzła kratownicy płaskiej możliwe jest napisanie dwóch statycznych równań równowagi (suma rzutów sił na oś X i suma rzutów sił na oś y), natomiast liczba niewiadomych do wyznaczenia jest równa liczbie prętów i reakcji, które trzeba wyznaczyć aby możliwe było obliczenie sił w prętach.
Gdy prawa strona równania [1] jest większa od lewej, kratownica jest niedosztywniona (czyli jest mechanizmem), w przeciwnym przypadku kratownica jest przesztywniona (statycznie niewyznaczalna).
Zadanie 1
Wyznaczyć reakcje kratownicy statycznie wyznaczalnej z rysunku 1 i obliczyć siły występujące w jej prętach.
Dane:
![a[m]; Q = /sqrt{2}[kN]; /alpha=45^{/circ}](rownania/w_078.gif)
Rozwiązanie:
Wyznaczenie reakcji podpór kratownicy za pomocą statycznych równań równowagi:
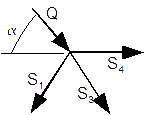
Teraz należy obliczyć siły w prętach kratownicy. W tym przypadku najlepiej zacząć od dowolnego węzła, w którym łączą się dwa pręty i kolejno rozpisując układy równań równowagi dla poszczególnych węzłów wyznaczać siły w prętach (kąty pomiędzy prętami kratownicy biegnącymi w na ukos są równe 60 i 30 stopni co wynika z rysunku 1).
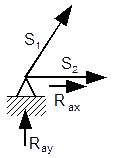 | |
 |
|
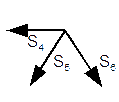 |
|
 |
Dodatkowe równanie, które stanowi jedynie sprawdzenie poprawności obliczenia siły S6: |
 |
Dodatkowe równanie, które stanowi jedynie sprawdzenie poprawności obliczenia sił S2, S3, S5 oraz S7: |
Zadanie 2
Obliczyć reakcje i siły w prętach kratownicy statycznie wyznaczalnej z rysunku 2.
Dane:
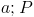
Rozwiązanie:
Równania równowagi dla wyznaczenia reakcji podpór (kąty pomiędzy prętami kratownicy biegnącymi w poprzek są równe 45° co wynika z rysunku 2):
Równania równowagi dla węzła A:
Równania równowagi dla węzła 3:
Równania równowagi dla węzła 1:
Równanie równowagi dla węzła 2:
Siła S7=0 ponieważ pręt w którym owa siła występuje nie przenosi żadnego obciążenia.
Równania równowagi dla węzła 4:
Równanie sprawdzające poprawność obliczeń:
Równanie równowagi dla węzła B sprawdzające poprawność obliczeń:
Zadanie 3 - do samodzielnego rozwiązania.
Wyznaczyć reakcje i siły w prętach kratownicy statycznie wyznaczalnej z rysunku 3.
Dane:
![a=1[m]; Q1=20[N]; Q2=50[N]; Q3=21[N]; Q4=10[N]](rownania/w_106.gif)
Odpowiedzi:
Reakcje podpór:
Siły w prętach kratownicy można odczytać z rysunku 4.
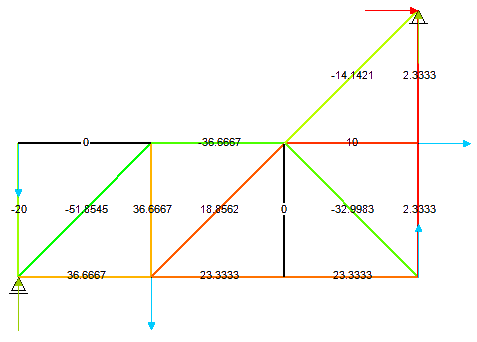
Zadanie 4
Wyznaczyć siły w prętach 6, 7, 8 kratownicy statycznie wyznaczalnej z zadania 3.Rozwiązanie:
Można oczywiście wyliczyć siły w prętach kratownicy metodą analityczną równoważenia węzłów (jak w zadaniach 1, 2 i 3), jednak nie oto chodzi żeby się katować niepotrzebnymi obliczeniami. Istnieje metoda przekrojów Rittera, która umożliwia szybkie wyznaczenie sił w wybranych prętach. Są jednak pewne ograniczenia, przekrój musi przecinać trzy pręty oraz wszystkie pręty nie mogą zbiegać się w jednym węźle. Jak wynika z rysunku 3, pręty w których siły należy wyliczyć spełniają te kryteria.
Po przecięciu kratownicy do wyboru do koloru mamy dwie możliwości:
liczyć siły w prętach z lewej strony przekroju kratownicy w następujący sposób (pomijam wyliczanie reakcji, ponieważ to była część zadania 3):
|
Suma momentów względem punktu I: |
Suma momentów względem punktu II:
Suma rzutów sił na oś Y:
lub z prawej strony przekroju kratownicy w analogiczny sposób:
|
Suma momentów względem punktu I |
Suma momentów względem punktu II:
Suma rzutów sił na oś Y:
Zadanie 5
Obliczyć metodą przekrojów Rittera siły S2, S6 i S5 prętów kratownicy z zadania 2.
Zadanie 6
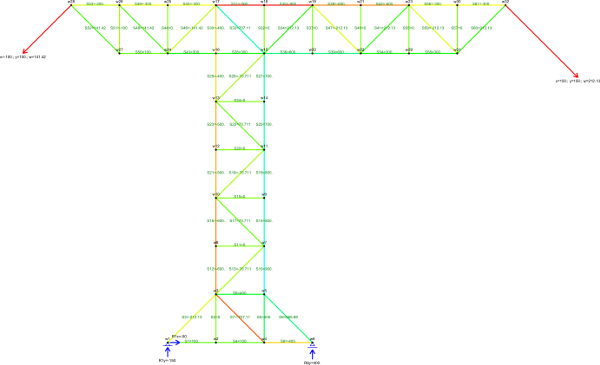
Obliczyć reakcje podpór i siły w trzech dowolnych prętach kratownicy statycznie wyznaczalnej z rysunku 5. Odległość pomiędzy sąsiadującymi węzłami kratownicy w poziomie i pionie jest taka sama i równa się 1 m. Siły dane zostały na rysunku.
Sprostowanie: nie jestem na tyle szalony, aby liczyć taką kratownicę ręcznie, ale na tyle szalony, aby napisać własny program, który tę kratownicę rozwiązał za mnie, narysował i pręty pokolorował. Mało tego, ten sam program rozpisał równania dla poszczególnych węzłów, których tutaj nie przytoczę, bo w końcu to jest część zadania.
Zadanie 7
Obliczyć reakcje i siły w prętach kratownicy statycznie wyznaczalnej z rysunku 6. Odległość pomiędzy sąsiadującymi w poziomie i pionie węzłami wynosi 1 m.
Układy równań:
Węzeł: 1
Węzeł: 2
Węzeł: 3
Węzeł: 4
Węzeł: 5
Węzeł: 6
Zadanie 8
Obliczyć reakcje i siły w prętach kratownicy statycznie wyznaczalnej z rysunku 7. Odległość pomiędzy sąsiadującymi w poziomie i pionie węzłami wynosi 1 m.
Układy równań:
Węzeł: 1
Węzeł: 2
Węzeł: 3
Węzeł: 4
Węzeł: 5
Węzeł: 6
Węzeł: 7
Węzeł: 8
Zadanie 9
Obliczyć reakcje i siły w prętach kratownicy statycznie wyznaczalnej z rysunku 8. Odległość pomiędzy sąsiadującymi w poziomie 1 m a w pionie 1,5 m.
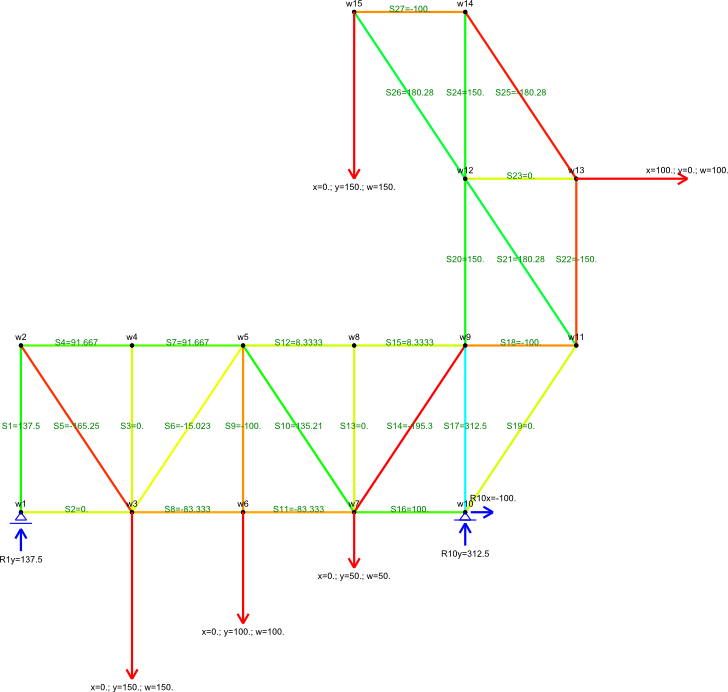
Węzeł: 1
Węzeł: 2
Węzeł: 3
Węzeł: 4
Węzeł: 5
Węzeł: 6
Węzeł: 7
Węzeł: 8
Węzeł: 9
Węzeł: 10
Węzeł: 11
Węzeł: 12
Węzeł: 13
Węzeł: 14
Węzeł: 15
Zadanie 10
Oblicz reakcje sił w prętach kratownicy statycznie wyznaczalnej z rysunku 9, w której odległość pomiędzy prętami pionowymi wynosi 1 m a długości prętów pionowych wynosi: L7=L10=100, L9=L12=145, L14=L18=170, L20=180.
Równania:
Węzeł: 1
Węzeł: 2
Węzeł: 3
Węzeł: 4
Węzeł: 5
Węzeł: 6
Węzeł: 7
Węzeł: 8
Węzeł: 9
Węzeł: 10
Węzeł: 11
Węzeł: 12
Węzeł: 13
Węzeł: 14
Zadanie 11
Oblicz reakcje sił w prętach kratownicy statycznie wyznaczalnej z rysunku 10, w której odległość pomiędzy sąsiadującymi węzłami w poziomie i pionie wynosi 1 m.
Równania:
Węzeł: 1
Węzeł: 2
Węzeł: 3
Węzeł: 4
Węzeł: 5
Węzeł: 6
Węzeł: 7
Węzeł: 8
Węzeł: 9
Węzeł: 10
Węzeł: 11
Węzeł: 12
Węzeł: 13
Węzeł: 14
Węzeł: 15
Węzeł: 16
Węzeł: 17
Węzeł: 18

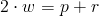
![/Sigma X = 0: R_{ax} + Q/cdot /frac{1}{/sqrt{2}} = 0 => R_{ax} = -1[kN]](https://obliczeniowo.com.pl/rownania/w_079.gif)
![/Sigma M_B = 0: R_{ay}/cdot 2/cdot a -Q /cdot /frac{1}{/sqrt{2}}/cdot 1/frac{1}{2}+Q/cdot /frac{1}{/sqrt{2}}/cdot /frac{/sqrt{3}}{2}/cdot a=0/Rightarrow R_{ay}=/frac{3-/sqrt{3}}{4}/approx 0.684[kN]](https://obliczeniowo.com.pl/rownania/w_080.gif)
![/Sigma Y = 0:R_{ay}+R_{by}-Q/cdot /frac{1}{/sqrt{2}}=0/Rightarrow R_{ay}=/frac{1+/sqrt{3}}{4}/approx 0.317[kN]](https://obliczeniowo.com.pl/rownania/w_081.gif)
![/Sigma Y = 0: S_1/cdot /frac{/sqrt{3}}{2}+R_{ay}=0/RightarrowS_1=/frac{R_{ay}}{/frac{/sqrt{3}}{2}}/approx -0.366[kN]](https://obliczeniowo.com.pl/rownania/w_082.gif)
![/Sigma X=0: S_2+R_{ax}+S_1/cdot /frac{1}{2}=0/Rightarrow S_2=1+0,366/cdot /frac{1}{2}/approx 1,168[kN]](https://obliczeniowo.com.pl/rownania/w_083.gif)
![/Sigma Y=0: -S_1/cdot /frac{/sqrt{3}}{2}-S_3/cdot /frac{/sqrt{3}}{2}-Q/cdot /frac{1}{/sqrt{2}}=0/Rightarrow S_3=/frac{-S_1/cdot /frac{/sqrt{3}}{2}-Q/cdot/frac{1}{/sqrt{2}}}{/frac{/sqrt{3}}{2}}/approx -0.789[kN]](https://obliczeniowo.com.pl/rownania/w_084.gif)
![/Sigma/, X=0:S_4+S_3/cdot/frac{1}{2}-S_1/cdot/frac{1}{2}+Q/cdot /frac{1}{/sqrt{2}}=0/Rightarrow S_4=-S_3/cdot/frac{1}{2}+S_3/cdot /frac{1}{2}-Q/cdot /frac{1}{/sqrt{2}}/approx -0.789[kN]](https://obliczeniowo.com.pl/rownania/w_085.gif)
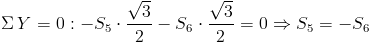
![/Sigma/, X=0: -S_5/cdot/frac{1}{2}+S_6/cdot/frac{1}{2}-S_4=0/Rightarrow S_6=S_4=-0.789[kN]/Rightarrow S_5=0,789[kN]](https://obliczeniowo.com.pl/rownania/w_087.gif)
![/Sigma/, X=0: -S_7-S_6/cdot /frac{1}{2}=0/Rightarrow S_7=-/frac{1}{2}/cdot S_6/approx 0.394[kN]](https://obliczeniowo.com.pl/rownania/w_088.gif)
![/Sigma/, Y=0:S_6/cdot /frac{/sqrt{3}}{2}+R_{by}=0/Rightarrow S_6=-/frac{R_{by}}{/frac{/sqrt{3}}{2}}/approx -0.789[kN]](https://obliczeniowo.com.pl/rownania/w_089.gif)
![/Sigma/, X=0: -S_2-S_3/cdot /frac{1}{2}+S_5/cdot /frac{1}{2}+S_7=-1.168+0.789/cdot /frac{1}{2}+0.789/cdot /frac{1}{2}+0.394=0[kN]](https://obliczeniowo.com.pl/rownania/w_090.gif)
![/Sigma/, Y=0: S_3/cdot /frac{/sqrt{3}}{2}+S_5/cdot /frac{/sqrt{3}}{2}=-0.789/cdot /frac{/sqrt{3}}{2}+0.789/cdot /frac{/sqrt{3}}{2}=0[kN]](https://obliczeniowo.com.pl/rownania/w_091.gif)
![/sum M_B=0:R_{Ay}/cdot 3/cdot a-P/cdot 2/cdot a+2/cdot P/cdot a=0/Rightarrow R_{Ay}=0[kN]](https://obliczeniowo.com.pl/rownania/w_093.gif)
![/sum Y=0: R_{Ay}-P+R_{By}=0/Rightarrow R_{By}=P[kN]](https://obliczeniowo.com.pl/rownania/w_094.gif)
![/sum X=0: R_{Bx}+2/cdot P=0/Rightarrow R_{Bx}=-2/cdot P[kN]](https://obliczeniowo.com.pl/rownania/w_095.gif)
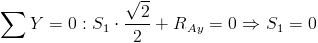
![/sum X=0: S_2=0[kN]](https://obliczeniowo.com.pl/rownania/w_097.gif)
![/sum X=0: -S_1/cdot/frac{/sqrt{2}}{2}+S_4=0/Rightarrow S_4=0[kN]](https://obliczeniowo.com.pl/rownania/w_098.gif)
![/sum Y=0: -S_1/cdot/frac{/sqrt{2}}{2}-S_3-P=0/Rightarrow S_3=-P[kN]](https://obliczeniowo.com.pl/rownania/w_099.gif)
![/sum Y=0: S_3+S_5/cdot/frac{/sqrt{2}}{2}=0/Rightarrow S_5=P/cdot/sqrt{2}[kN]](https://obliczeniowo.com.pl/rownania/w_100.gif)
![/sum X=0: -S_2+S_6+S_5/cdot/frac{/sqrt{2}}{2}=0/Rightarrow S_6=-P[kN]](https://obliczeniowo.com.pl/rownania/w_101.gif)
![/sum X=0: -S_6+S_8=0/Rightarrow S_8=-P[kN]](https://obliczeniowo.com.pl/rownania/w_102.gif)
![/sum Y=0: -S_5/cdot /frac{/sqrt{2}}{2}-S_7-S_9/cdot/frac{/sqrt{2}}{2}=0/Rightarrow S_9-S_5=-P/cdot /sqrt{2}[kN]](https://obliczeniowo.com.pl/rownania/w_103.gif)
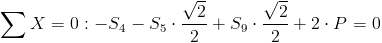
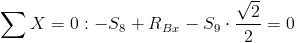
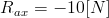
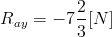
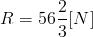
![Suma MI=0: -S6*a+Q1*a-R*a=0=>S6=-36 2/3[N]](https://obliczeniowo.com.pl/rownania/w_110.gif)
![Suma MII=0: S8*a+Q1*2*a+Q2*a-R*2*a=0=>S8=-23 1/3[N]](https://obliczeniowo.com.pl/rownania/w_111.gif)
![Suma Y=0: S7*2^0,5/2-Q1+r-q2=0=>S7=13 1/3[N]](https://obliczeniowo.com.pl/rownania/w_112.gif)
![Suma MI=0: S6*a-Q4*a-+Q3*2*a-Ray*2*a+Rax*2*a=0=>S6=-36 2/3[N]](https://obliczeniowo.com.pl/rownania/w_113.gif)
![Suma MII=0: -S8+Q3*a+Ray*a-Rax*a=0=>S8=-23 1/3[N]](https://obliczeniowo.com.pl/rownania/w_114.gif)
![Suma Y=0: -S7*2^0,5/2+Q3+Ray=0=>Ray=13 1/3*2^0,5[N]](https://obliczeniowo.com.pl/rownania/w_115.gif)