Sprawdzenie, czy punkt należy do elipsy
Stronę tą wyświetlono już: 922 razy
Jeżeli dana jest elipsa o następujących parametrach:
- rx - promień na osi x;
- ry - promień na osi y;
- xc i yc - współrzędne środka elipsy;
i dany jest punkt P, to tenże punkt P leży na obrzeżu lub we wnętrzu elipsy wtedy i tylko wtedy, gdy spełniony jest poniższy warunek:
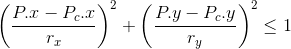 | [1] |
Zapis wyrażenia w formacie TeX-a:
\left(\frac{P.x-P_c.x}{r_x}\right)^2+\left(\frac{P.y-P_c.y}{r_y}\right)^2\le 1
gdzie:
P.x i P.y to oczywiście współrzędne punktu P.
Aby możliwe było określenie, czy punkt należy do elipsy, która została obrócona, konieczna jest znajomość dodatkowego parametru, którym jest kąt obrotu α. Kąt ten zawarty jest pomiędzy prostą równoległą do osi x przechodzącą przez środek elipsy a promieniem rx obróconej elipsy (jak pokazane zostało na poniższym rysunku). W takim przypadku można skorzystać z warunku [1] dla elipsy nieobróconej jedyne co należy zrobić, to obrócić punkt P w przeciwnym kierunku o kąt α względem punktu centralnego tejże elipsy.
