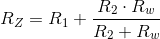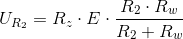Pomiar napięcia U

Stronę tą wyświetlono już: 4886 razy

Pomiar napięcia może być wykonywany poprzez bezpośrednie podłączenie woltomierza do obwodu elektrycznego lub równoległe podłączenie względem odbiornika. Dzieje się tak ponieważ woltomierze charakteryzują się dużą rezystancją własną R_w a co za tym idzie małym poborem prądu I. W niektórych przypadkach przeprowadzania pomiarów rezystancja własna R_w wpływa na wynik pomiarowy. Poniżej znajduje się schemat podłączenia przyrządu pomiarowego bezpośrednio do źródła napięcia.

W przypadku podłączonego do źródła zasilania odbiornika nie należy podłączać woltomierza szeregowo, gdyż taki sposób podłączenia może doprowadzić do uszkodzenia przyrządu a także sam pomiar nie będzie miał nic wspólnego z rzeczywistym napięciem U płynącym przez odbiornik O. Przykład schematu poprawnego podłączenia woltomierza do układu z odbiornikiem O można zobaczyć poniżej.

W przypadku pomiaru napięcia U w dzielnikach napięcia duży wpływ na wynik pomiaru odgrywać będzie rezystancja wewnętrzna R_w przyrządu pomiarowego. Dzieje się tak, gdyż równoległe wpięcie do obwodu woltomierza powoduje zmianę rezystancji układu a więc i rozkładu napięć na dzielniku. Przykład pomiaru, w którym istotną rolę odgrywa rezystancja wewnętrzna R_w przyrządu pomiarowego został pokazany na poniższym rysunku.

W powyższym przypadku rezystancja zastępcza całego układu będzie równa:

[1]

Zapis wyrażenia w formacie TeX-a:

R_{Z}=R_1+\frac{R_2\cdot R_w}{R_2 + R_w}

Napięcie U_R2 w układzie z powyższego rysunku będzie więc równe:

[2]

Zapis wyrażenia w formacie TeX-a:

U_{R_2} = R_z\cdot E \cdot \frac{R_2\cdot R_w}{R_2 + R_w}

gdzie:

• E - napięcie źródła zasilania;
• R_w - rezystancja wewnętrzna woltomierza;
• R₂ - rezystancja opornika, dla którego napięcie U_Rw jest mierzone;
• R₁ - rezystancja opornika pierwszego;
• R_z - rezystancja zastępcza całego układu z podpiętym woltomierzem;
• R_z · E - to wyrażenie oblicza natężenie I prądu płynącego przez układ.

Gdy rezystancja wewnętrzna R_w dąży do nieskończoności to:

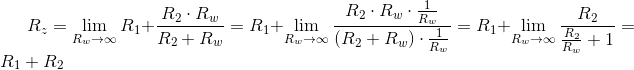[3]

Zapis wyrażenia w formacie TeX-a:

R_z=\lim_{R_w\rightarrow \infty}R_1+\frac{R_2\cdot R_w}{R_2 + R_w}=R_1+\lim_{R_w\rightarrow \infty}\frac{R_2\cdot R_w \cdot \frac{1}{R_w}}{(R_2+R_w)\cdot\frac{1}{R_w}}=R_1+\lim_{R_w\rightarrow \infty}\frac{R_2}{\frac{R_2}{R_w}+1}=R_1+R_2

Z powyższego wynika, że im większa rezystancja wewnętrzna przyrządu pomiarowego, tym mniejszy błąd pomiarowy, gdyż wartość rezystancji zastępczej równolegle podłączonych elementów oporowych dąży do najniższej rezystancji tego układu, gdy oporność drugiego z nich dąży do nieskończoności. Z tego też względu należy zwracać w przyrządach pomiarowych uwagę na parametr rezystancji wewnętrznej R_w, który może mieć istotny wpływ na wynik pomiaru.