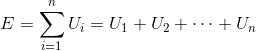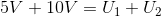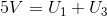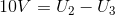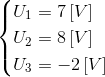II prawo Kirchhoffa
Stronę tą wyświetlono już: 18985 razy
II prawo Kirchhoffa umożliwia obliczanie napięcia płynącego przez układy połączone szeregowo, które są zasilane prądem stałym. Tak więc II prawo Kirchhoffa mówi, że: W dowolnym oczku obwodu elektrycznego prądu stałego suma spadków napięcia U na poszczególnych elementach rezystancyjnych jest równa sumie sił elektromotorycznych E działających w tym oczku.
Powyższe prawo można zapisać w następujący sposób:
Oczkiem obwodu elektrycznego nazywa się jedną z możliwych dróg przepływu prądu elektrycznego
Na poniższej ilustracji pokazany został układ zawierający dwa źródła zasilania i trzy oczka przepływu prądu: ABCD; ABD; CBD
Suma spadków napięcia w oczku ABCD będzie więc równa:
Suma spadków napięcia w oczku ABD będzie więc równa:
Suma spadków napięcia w oczku CBD będzie więc równa:
Choć równania [2], [3] i [4] są prawdziwe to do obliczenia takiego układu konieczne jest uzależnienie napięcia U1, U2 i U3 odpowiednio od natężenia I1, I2, I3 oraz rezystancji R1, R2 oraz R3. Tak więc potrzebne są dwa równania napięciowe wynikające z II prawa Kirchhoffa i jedno natężeniowe wynikające z I prawa Kirchhoffa:
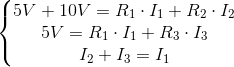 | [5] |
Zapis wyrażenia w formacie TeX-a:
Załóżmy więc, że elementy układu z rysunku 1 mają odpowiednio rezystancję R1 = R2 = 4,5[Ω]; R3 = 9 [Ω], wtedy to natężenia prądu będą równe:
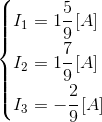 | [6] |
Zapis wyrażenia w formacie TeX-a:
Z kolei napięcia występujące na elementach obwodu: