Stronę tą wyświetlono już: 9291 razy

Niechaj Ω składa się z n zdarzeń elementarnych jednakowo prawdopodobnych i niechaj zdarzenie losowe A⊂Ω. W takowym przypadku każdemu zdarzeniu losowemu A przyporządkowujemy liczbę P(A) zwaną prawdopodobieństwem zajścia zdarzenia A i spełniającą warunki:

1) P(A)≥0;

2) P(A)=P(Ω)=1 - prawdopodobieństwo zdarzenia pewnego;

3) P(A∪B)=P(A)+P(B) (założenie A∩B=ϕ) - prawdopodobieństwo zdarzeń wykluczających się jest równe sumie prawdopodobieństwa tych zdarzeń.

Właściwości prawdopodobieństwa:

1) Prawdopodobieństwo zdarzenia, któremu nie sprzyja żadne zdarzenie elementarne jest równe zeru P(ϕ)=0;

2) Prawdopodobieństwo dwóch zdarzeń A i B jest równe sumie prawdopodobieństw tych zdarzeń pomniejszonej o prawdopodobieństwo części wspólnej tych zdarzeń P(A∪B)=P(A)+P(B)-P(A∩B);

Prawdopodobieństwo zdarzenia przeciwnego do zdarzenia A jest równe różnicy prawdopodobieństwa zdarzenia pewnego (którego wartość wynosi 1) i zdarzenia A czyli P(A')=1-P(A)

Zadanie 1

W urnie są 4 kule białe i 5 kul czarnych. Losowo wybrano dwie kule. Oblicz jakie jest prawdopodobieństwo wylosowania kul tego samego koloru.

Rozwiązanie:

Doświadczenie dwuetapowe. Zbiór Ω tworzą dwuelementowe kombinacje bez powtórzeń zbioru 9-cio elementowego.

[1]

Zapis wyrażenia w formacie TeX-a:

\overline{\overline{\Omega}}=C_{9}^{2}=\frac{9!}{2!\cdot(9-2)!}=36

A - zdarzenie w którym wylosowano kule tego samego koloru (A₁ - dwie kule białe lub A₂ - dwie kule czarne).

Możemy zapisać, że zdarzenie A=A₁+A₂. Przy czym część wspólna zbiorów A₁∪A₂=ϕ (jest zbiorem pustym). Tym samym w tym przypadku prawdopodobieństwo zdarzenia A jest równe:

[2]

Zapis wyrażenia w formacie TeX-a:

P(A)=P(A_1\cup A_2)=P(A_1)+P(A_2)=\frac{\overline{\overline{A_1}}}{\overline{\overline{\Omega}}}+\frac{\overline{\overline{A_2}}}{\overline{\overline{\Omega}}}

Obliczamy liczebność zbiorów A₁ i A₂:

[3]

Zapis wyrażenia w formacie TeX-a:

P(A_1)=C_4^2=\frac{4!}{2!\cdot(4-2)!}=6

[4]

Zapis wyrażenia w formacie TeX-a:

P(A_2)=C_5^2=\frac{5!}{2!\cdot(5-2)!}=10

Pozostaje jedynie podstawić do zależności [2]:

[5]

Zapis wyrażenia w formacie TeX-a:

P(A)=\frac{6}{36}+\frac{10}{36}=\frac{4}{9} \approx 44,4\%

Prawdopodobieństwo wylosowania kul tego samego koloru jest równe w przybliżeniu 44,4%

Zadanie 2

Z talii 24 kart losowo wybrano jedną. Jakie jest prawdopodobieństwo wylosowania kiera lub karty koloru czerwonego.

Rozwiązanie:

Doświadczenie jednoetapowe, więc overline{overline{Omega}}=24.

A zdarzenie, w którym wylosowano kiera (A₁) lub wylosowano kartę koloru czerwonego (A₂)

Rozwiązaniem jest P(A)=P(A₁∩A₂).

Liczebność zbioru A₁ wynosi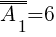

Liczebność zbioru A₂ wynosi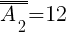

Część wspólna zbiorów A₁∩A₂ wynosi overline{overline{A_{1} inter A_{2}}}=6.

Teraz, skoro wszystko już wiadomo można policzyć prawdopodobieństwo zdarzenia A:

[6]

Zapis wyrażenia w formacie TeX-a:

P(A)=P(A_1)+P(A_2)-P({A}_{1}\cap A_2)=\frac{\overline{\overline{A_1}}}{\overline{\overline{\Omega}}}+\frac{\overline{\overline{A_2}}}{\overline{\overline{\Omega}}}-\frac{\overline{\overline{A_1\cap A_2}}}{\overline{\overline{\Omega}}}=\frac{6}{34}+\frac{12}{24}-\frac{6}{12}=\frac{1}{2}=50\%

Prawdopodobieństwo wylosowania kiera lub karty koloru czerwonego jest równe 50%