Prawdopodobieństwo zdarzeń warunkowych
Stronę tą wyświetlono już: 3531 razy
Prawdopodobieństwem zajścia zdarzenia A pod warunkiem zajścia zdarzenia B nazywa się liczbę 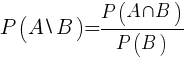 przy założeniu, że P(B)>0.
przy założeniu, że P(B)>0.
Zadanie 1
Wykonujemy rzut kostką do gry. Oblicz prawdopodobieństwo wyznaczenia parzystej liczby oczek pod warunkiem wyrzucenia co najmniej 5-ciu oczek.
Rozwiązanie:
Doświadczenie jednoetapowe 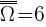
AB - zdarzenie, w którym wyrzucono parzystą liczbę oczek pod warunkiem wyrzucenia co najwyżej 5-ciu oczek.
A - zdarzenie, w którym wyrzucono parzystą liczbę oczek A={2; 4; 6}, 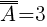 .
.
B - zdarzenie, w którym wyrzucono co najwyżej pięć oczek B={1; 2; 3; 4; 5}, 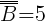 .
.
A∪B - zdarzenie, w którym wyrzucono parzystą liczbę oczek i co najwyżej pięć oczek. A∪B = {2; 4}, 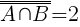
Obliczanie prawdopodobieństwa:
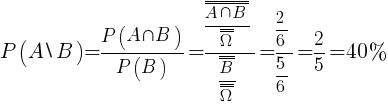 |
[1] |
Prawdopodobieństwo wyrzucenia parzystej liczby oczek pod warunkiem wyrzucenia co najwyżej pięciu oczek jest równe 40%
Zadanie 2
W pojemniku znajdują się 3 kule białe, 2 czarne i 4 zielone. Losowo wybrano 2 kule. Oblicz prawdopodobieństwo wyboru kuli białej pod warunkiem, że pierwsza wylosowana kula była zielona.
Rozwiązanie:
Doświadczenie dwuetapowe:
Etap I - losowanie pierwszej kuli 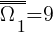 ;
;
Etap II - losowanie pierwszej kuli 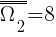 .
.
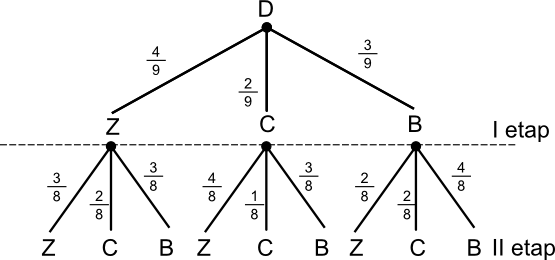
AB - zdarzenie, w którym wylosowano kulę białą pod warunkiem, że za pierwszym razem wylosowano kulę zieloną.
A - zdarzenie, w którym za pierwszym razem wylosowano kulę zieloną.
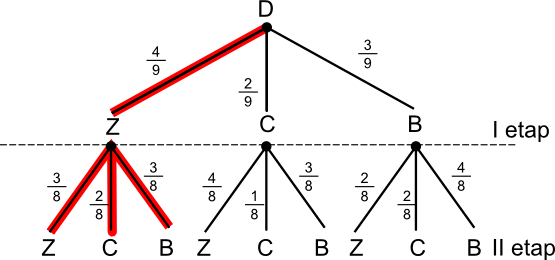
Prawdopodobieństwo zdarzenia B:
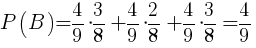 |
[2] |
A∪B - wylosowano jedną białą i za pierwszym razem wylosowano zieloną.
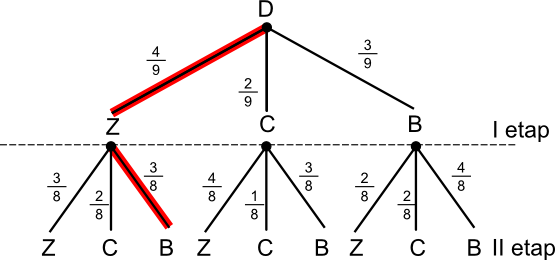
Prawdopodobieństwo zdarzenia A∪B jest równe:
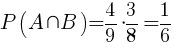 |
[3] |
Teraz można już obliczyć prawdopodobieństwo warunkowe:
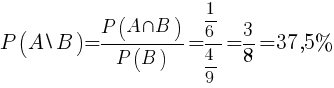 |
[4] |
Zadanie 3
W urnie znajduje się 20 kul, wśród których jest: 8 kul białych z cyfrą 1; 7 kul białych z cyfrą 2; 3 kule czarne z cyfrą 1 i 2 kule czarne z cyfrą 2. Losowo wybieramy jedną kulę. Oblicz jakie jest prawdopodobieństwo wylosowania kuli białej pod warunkiem wylosowania kuli z cyfrą 2.
Rozwiązanie:
Doświadczenie dwuetapowe:
Etap I - losuję kulę ze względu na kolor 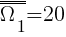 ;
;
Etap II - sprawdzam kulę ze względu na jej numer, zbiór dla białych 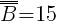 , zbiór dla czarnych
, zbiór dla czarnych 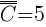 ;
;
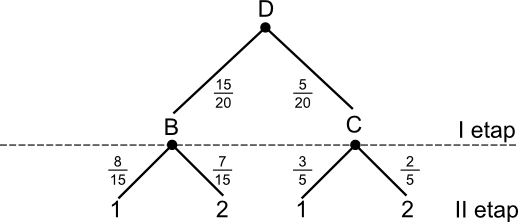
AB - zdarzenie, w którym wylosowano kulę białą pod warunkiem, że wylosowano kulę z cyfrą 2.
A - zdarzenie, w którym wylosowano kulę białą
B - zdarzenie, w którym wylosowano kulę z cyfrą 2
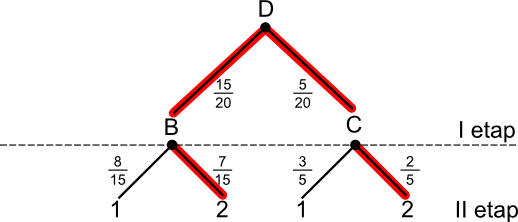
Prawdopodobieństwo zdarzenia A wynosi:
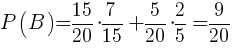 |
[5] |
A∪B - zdarzenie, w którym wylosowano kulę białą z cyfrą 2.
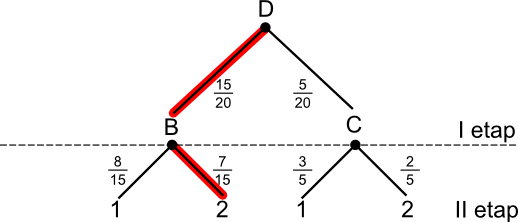
Prawdopodobieństwo zdarzenia AB jest więc równe:
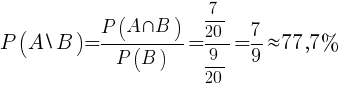 |
[6] |

Tytuł:
Matematyka w uczeniu maszynowym
Autor:
Marc Peter Deisenroth, A. Aldo Faisal, Cheng Soon Ong

Tytuł:
Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie
Autor:
Ryan T. White, Archana Tikayat Ray

Tytuł:
Matematyka w Pythonie. Algebra, statystyka, analiza matematyczna i inne dziedziny
Autor:
Amit Saha

Tytuł:
Matematyka dla menedżerów. Wydanie II
Autor:
Michael C. Thomsett

Tytuł:
Matematyka Poradnik encyklopedyczny
Autor:
I.N. Bronsztejn, K.A. Siemiendiajew

Tytuł:
Matematyka finansowa
Autor:
Jacek Jakubowski, Andrzej Palczewski, Marek Rutkowski, Łukasz Stettner

Tytuł:
Proste jak pi Matematyka to bułka z masłem
Autor:
Liz Strachan

Tytuł:
O twierdzeniach i hipotezach. Matematyka według Delty
Autor:
Witold Sadowski, Wiktor Bartol

Tytuł:
Matematyka dla biologów
Autor:
Dariusz Wrzosek

Tytuł:
Matematyka dla programistów Java
Autor:
Jacek Piechota
