Obliczanie prawdopodobieństwa zdarzeń metodą drzewa

Stronę tą wyświetlono już: 44211 razy

Metodę drzewa stosuje się w doświadczeniach wieloetapowych. Każde doświadczenie wieloetapowe dzieli się na pojedyncze etapy (próby lub doświadczenia cząstkowe), każdy etap rozpatrujemy oddzielnie

Przykład

Wykonujemy niczym Harwey Dent trzy rzuty monetą.

Mamy tutaj do czynienia z doświadczeniem trój etapowym:

I etap - rzut monetą $overline{overline{Omega_{1}}}=2$ ;

II etap - rzut monetą 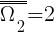$overline{overline{Omega_{2}}}=2$ ;

III etap - rzut monetą 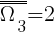$overline{overline{Omega_{3}}}=2$ ;

Rys. 1
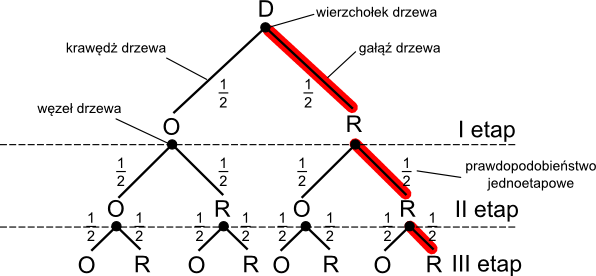
Przykład budowy drzewa stworzonego dla rozpatrywanego przykładu.

Opis drzewa:

1) punkt wspólny krawędzi nazywa się węzłem;

2) każda gałąź drzewa składa się z ciągu krawędzi;

3) punkt wspólny wszystkich gałęzi nazywa się wierzchołkiem drzewa;

4) każdej krawędzi przypisuje się prawdopodobieństwo pewnego doświadczenia jednoetapowego.

Zasady obliczania prawdopodobieństw z drzewa

1) Zasada mnożenia - prawdopodobieństwo jednej gałęzi jest równe iloczynowi prawdopodobieństw przypisanych krawędziom, z których dana krawędź się składa.

A - zdarzenie, w którym wypadły same reszki

Prawdopodobieństwo tego zdarzenia jest równe:

[1]

Zapis wyrażenia w formacie TeX-a:

P(A)=\frac{1}{2}\cdot\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{8}

b) Zasada dodawania - jeżeli pewnemu zdarzeniu losowemu odpowiada więcej niż jedna gałąź to prawdopodobieństwo takiego zdarzenia jest równe sumie prawdopodobieństw poszczególnych gałęzi.

B - zdarzenie, w którym wypadły dokładnie dwie reszki.

Prawdopodobieństwo takiego zdarzenia jest równe:

[2]

Zapis wyrażenia w formacie TeX-a:

P(B)=\frac{1}{2}\cdot\frac{1}{2}\cdot\frac{1}{2}+\frac{1}{2}\cdot\frac{1}{2}\cdot\frac{1}{2}+\frac{1}{2}\cdot\frac{1}{2}\cdot\frac{1}{2}=\frac{3}{8}

Zadanie 1

Z talii 52 kart losowo wybrano trzy karty. Jakie jest prawdopodobieństwo wyboru co najmniej jednego kiera?

Rozwiązanie:

Doświadczenie trój etapowe:

I etap: - losowanie jednej karty bez zwracania $overline{overline{Omega_{1}}}=52$ ;

II etap: - losowanie jednej karty bez zwracania $overline{overline{Omega_{1}}}=51$ ;

III etap: - losowanie jednej karty bez zwracania 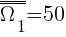$overline{overline{Omega_{1}}}=50$ ;

Stosuję metodę drzewa

A - zdarzenie, w którym wylosowano co najmniej jednego kiera (temu zdarzeniu sprzyja 7 gałęzi drzewa co zostało zaznaczone na rysunku 2.

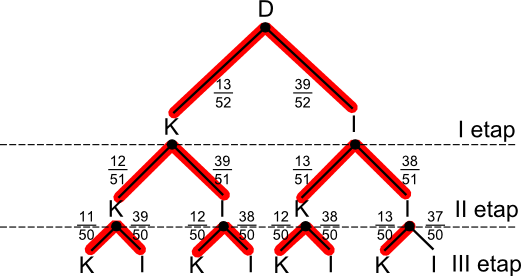
Drzewo z zaznaczonymi na czerwono gałęziami sprzyjającymi zajściu zdarzenia <b>A</b>. — Rys. 2
Drzewo z zaznaczonymi na czerwono gałęziami sprzyjającymi zajściu zdarzenia A.

Prawdopodobieństwo zdarzenia A jest równe:

[3]

Zapis wyrażenia w formacie TeX-a:

P(A)=\frac{13}{52}\cdot\frac{12}{51}\cdot=\frac{11}{50}+\frac{13}{52}\cdot\frac{12}{51}\cdot\frac{39}{50}+\frac{13}{52}\cdot\frac{39}{51}\cdot\frac{12}{50}+\frac{13}{52}\cdot\frac{39}{51}\cdot\frac{38}{50}+\frac{39}{52}\cdot\frac{13}{51}\cdot\frac{12}{50}+\frac{39}{52}\cdot\frac{13}{51}\cdot\frac{38}{50}+\frac{39}{52}\cdot\frac{38}{51}\cdot\frac{13}{50}=\frac{997}{1700}\approx 58,6\%

W tym przypadku jednak łatwiej jest posłużyć się zdarzeniem przeciwnym A', któremu sprzyja tylko jedna gałąź drzewa, co zostało pokazane na rysunku 3.

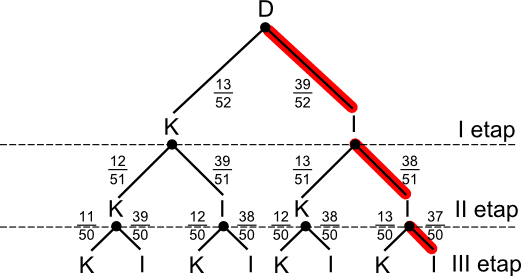
Prawdopodobieństwo zdarzenia A można obliczyć korzystając z prawdopodobieństwa zdarzenia przeciwnego A' w następujący sposób:

[4]

Zapis wyrażenia w formacie TeX-a:

P(A)=1-P(A ')=1-\frac{39}{52}\cdot\frac{38}{51}\cdot\frac{37}{50}=1-\frac{703}{1700}=\frac{997}{1700}\approx 58,6\%

Prawdopodobieństwo wylosowania co najmniej jednego kiera wynosi 58,6%

Zadanie 2

W urnie znajdują się 4 kule białe i 6 kul zielonych. Losowo wybrano 2 kule. Oblicz prawdopodobieństwo wybrania: a) kul tego samego koloru; b) kul różnokolorowych; c) co najwyżej jednej białej.

Rozwiązanie:

Doświadczenie dwuetapowe:

Etap I - losowanie kuli z 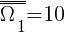$overline{overline{Omega_{1}}}=10$

Etap II -losowanie kuli z 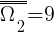$overline{overline{Omega_{2}}}=9$

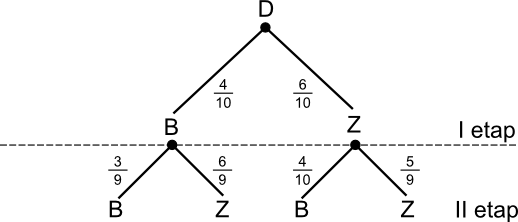
a) - zdarzenie, w którym wylosowano kule tego samego koloru. Dla tego zdarzenia rysunek drzewa z zaznaczonymi gałęziami został pokazany poniżej.

Drzewo z zaznaczonymi gałęziami sprzyjającymi zajściu zdarzenia <b>A</b>. — Rys. 5
Drzewo z zaznaczonymi gałęziami sprzyjającymi zajściu zdarzenia A.

Korzystając z rysunku 5 obliczamy prawdopodobieństwo zdarzanie A

[5]

Zapis wyrażenia w formacie TeX-a:

P(A)=\frac{4}{10}\cdot\frac{3}{9}+\frac{6}{10}\cdot\frac{5}{9}=\frac{7}{15}

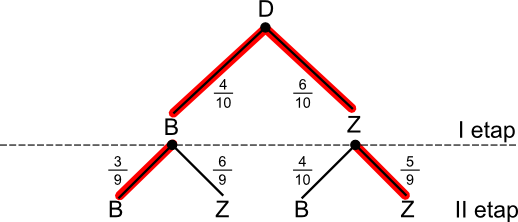
b) - zdarzenie, w którym wylosowano różnokolorowe kule.

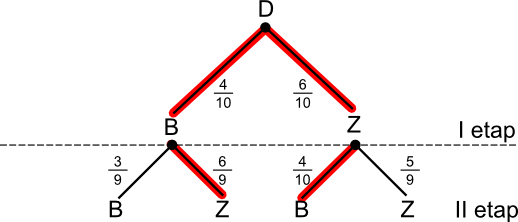
Drzewo z zaznaczonymi gałęziami sprzyjającymi zajściu zdarzenia <b>B</b>. — Rys. 6
Drzewo z zaznaczonymi gałęziami sprzyjającymi zajściu zdarzenia B.

Korzystając z rysunku 6 obliczamy prawdopodobieństwo zdarzanie B

[6]

Zapis wyrażenia w formacie TeX-a:

P(B)=\frac{4}{10}\cdot\frac{6}{9}+\frac{6}{10}\cdot\frac{4}{9}=\frac{8}{15}

Można też wykorzystać zdarzenie A do tego celu, ponieważ jest ono zdarzeniem przeciwnym do zdarzenia B

[7]

Zapis wyrażenia w formacie TeX-a:

P(B)=1-P(A)=1-\frac{7}{15}=\frac{8}{15}

c) zdarzenie, w którym wylosowano co najmniej jedną białą kulę.

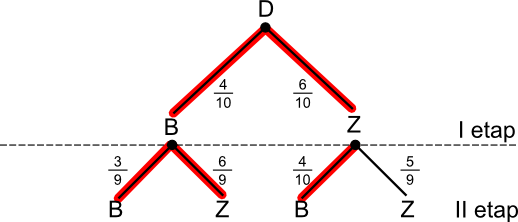
Drzewo z zaznaczonymi gałęziami sprzyjającymi zajściu zdarzenia <b>C</b>. — Rys. 7
Drzewo z zaznaczonymi gałęziami sprzyjającymi zajściu zdarzenia C.

Na rysunku 7 widać jak na dłoni, że lepiej będzie użyć do wyznaczanie prawdopodobieństwa zdarzenia C zdarzenia przeciwnego C', czyli takiego, w którym wylosowano tylko zielone kule.

[8]

Zapis wyrażenia w formacie TeX-a:

P(C)=1-P(C ')=1-\frac{6}{10}\cdot\frac{5}{9}=1-\frac{1}{3}=\frac{2}{3}

Zadanie 3

W urnie znajdują się piłeczki: m czerwonych i 6 zielonych. Losowo wyciągnięto dwie piłeczki. Prawdopodobieństwo tego, że obie są czerwone wynosi 0,5. Oblicz ile jest piłeczek czerwonych w urnie.

Rozwiązanie:

Doświadczenie dwuetapowe:

Etap I - losujemy I kulkę $overline{overline{Omega_{1}}}=m+6$ ;

Etap II - losujemy II kulkę 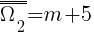$overline{overline{Omega_{2}}}=m+5$

A - zdarzenie, w którym wylosowano dwie czerwone piłeczki.

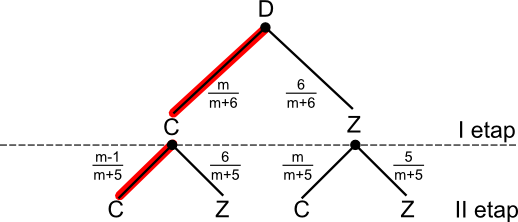
Ponieważ wiadomo, że P(A)=0,5 więc można napisać następujące równanie:

[9]

Zapis wyrażenia w formacie TeX-a:

\begin{matrix}\cfrac{m}{m+6}\cdot\cfrac{m-1}{m+5}=\cfrac{1}{2}\\ \\ \cfrac{m^2-m}{m^2+11\cdot m+30}=\cfrac{1}{2}\\ \\ 2\cdot m\cdot (m-1)=(m+6)\cdot(m+5)\\ \\ m^{2}-13\cdot m-30=0 \end{matrix}

Jak widać z rozpisania i uproszczenia zależności [9] otrzymane zostało równanie kwadratowe, dla którego konieczne jest znalezienie pierwiastków.

[10]

Zapis wyrażenia w formacie TeX-a:

\begin{matrix}\Delta=13^2-4\cdot 1\cdot (-30)=289\\ \\ \sqrt{\Delta}=17\\ \\ m_1=\cfrac{13-17}{2}=-2\\ \\ m_2=\cfrac{13+17}{2}=15 \end{matrix}

Założenia m&mt;1 i m∈N a więc m=15

Zadanie 4

W pierwszej urnie są dwie kule białe i trzy czarne (nie żebym był rasistą), natomiast w drugiej trzy czarne i pięć białych. Rzucamy kostką do gry, jeżeli wypadnie 6 oczek to losujemy kulę z urny pierwszej, w przeciwnym przypadku losujemy kulę z drugiej urny. Oblicz prawdopodobieństwo wylosowania kuli białej.

Rozwiązanie:

Doświadczenie dwuetapowe:

I etap - rzut kostką 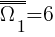$overline{overline{Omega_{1}}}=6$ ;

II etap - losowanie kuli z pierwszej urny U₁, dla którego $overline{overline{Omega_{2}}}=5$ lub z drugiej urny U₂, dla którego $overline(overline{Omega_{2}}}=8$ .

A - zdarzenie, w którym wylosowano kulę białą.

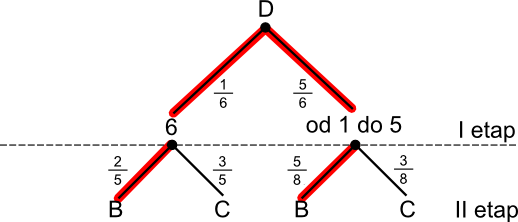
Prawdopodobieństwo zdarzenia A wynosi:

[11]

Zapis wyrażenia w formacie TeX-a:

P(A)=\frac{1}{6}\cdot\frac{2}{5}+\frac{5}{6}\cdot\frac{5}{8}=\frac{47}{80} = 58.75\%

Zadanie 5

Spośród liczb naturalnych spełniających nierówność 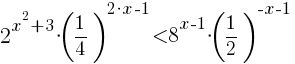$2^{x^{2}+3}*({{1}/{4}})^{2*x-1}<8^{x-1}*({{1}/{2}})^{-x-1}$ losujemy kolejno ze zwracaniem dwie liczby. Oblicz prawdopodobieństwo zdarzeń: A - w którym suma liczb wylosowanych jest mniejsza od dziesięciu; B - zdarzenie, w którym obie wylosowane liczby są równe.

Rozwiązanie:

Nierówność 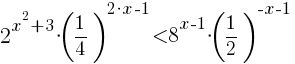$2^{x^{2}+3}*({{1}/{4}})^{2*x-1}<8^{x-1}*({{1}/{2}})^{-x-1}$ przekształcić należy do następującej postaci:

[12]

Zapis wyrażenia w formacie TeX-a:

2^{x^{2}-4\cdot x+5}<2^{4\cdotx-2}

Ponieważ podstawy potęg w nierówności [12] są sobie równe więc rozwiązaniem nierówności jest nierówność potęg:

[13]

Zapis wyrażenia w formacie TeX-a:

x^{2}-4\cdot x+5<4\cdot x-2

Po przekształceniu nierówności [13] otrzymujemy nierówność kwadratową:

[14]

Zapis wyrażenia w formacie TeX-a:

x^2-8\cdot x+7<0

Wyliczamy Δ i jej pierwiastek:

[15]

Zapis wyrażenia w formacie TeX-a:

\Delta=(-8)^2-4\cdot 7\cdot 1=36

Miejsca zerowe:

[16]

Zapis wyrażenia w formacie TeX-a:

x_1=\frac{8-6}{2\cdot 1}=1

Rys. 10

Poglądowy wykres funkcji wyznaczającej zbiór losowanych liczb (wypisanych pomiędzy x₁ a x₂).

Źródło:

Wykres wygenerowany przes skrypt PHP autora strony opisany na stronie Programowanie → Skrypty PHP → Skrypt PHP generujący wykres funkcji 2W

A więc tajemnica została rozwikłana, losujemy ze zbioru liczb {2; 3; 4; 5; 6}

Doświadczenie dwuetapowe:

Etap I - losowanie pierwszej liczby 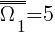$overline{overline{Omega_{1}}}=5$ ;

Etap II - losowanie drugiej liczby $overline{overline{Omega_{2}}}=5$ .

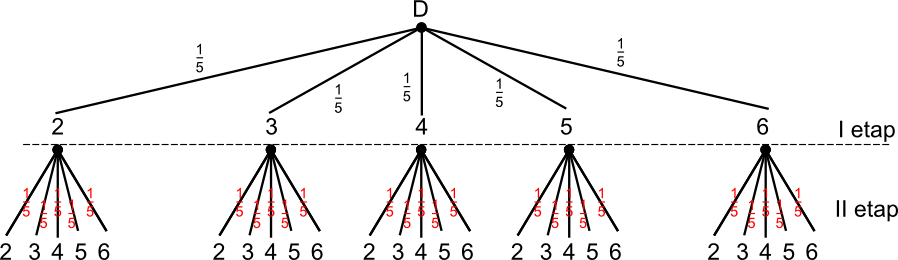
A - zdarzenie, w którym suma liczb wylosowanych jest mniejsza od 10.

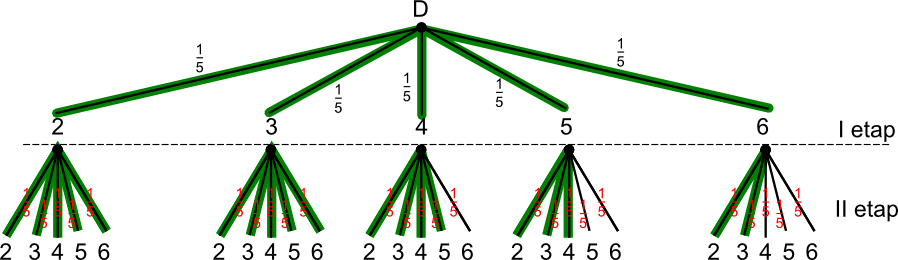
Prawdopodobieństwo zdarzenia A wynosi:

[17]

Zapis wyrażenia w formacie TeX-a:

P(A)=19\cdot\frac{1}{5}\cdot\frac{1}{5}=\frac{19}{25}

B - zdarzenie, w którym wylosowane liczby są sobie równe.

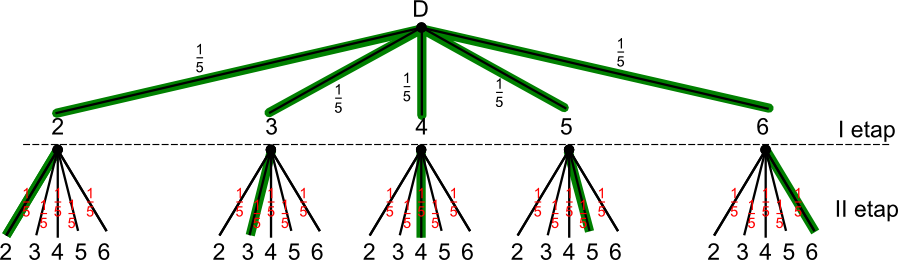
Prawdopodobieństwo zdarzenia B wynosi:

[18]

Zapis wyrażenia w formacie TeX-a:

P(A)=5\cdot\frac{1}{5}\cdot\frac{1}{5}=\frac{1}{5}

Propozycje książek

Tytuł:

Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie

Autor:

Ryan T. White, Archana Tikayat Ray

Tytuł:

Matematyka w Pythonie. Algebra, statystyka, analiza matematyczna i inne dziedziny

Autor:

Amit Saha

Tytuł:

Matematyka dla menedżerów. Wydanie II

Autor:

Michael C. Thomsett

Tytuł:

Matematyka Poradnik encyklopedyczny

Autor:

I.N. Bronsztejn, K.A. Siemiendiajew

Tytuł:

Matematyka finansowa

Autor:

Jacek Jakubowski, Andrzej Palczewski, Marek Rutkowski, Łukasz Stettner

Tytuł:

Sprawdziany Matematyka Klasa 3

Autor:

Iwona Kowalska, Beata Guzowska

Tytuł:

Proste jak pi Matematyka to bułka z masłem

Autor:

Liz Strachan

Tytuł:

O twierdzeniach i hipotezach. Matematyka według Delty

Autor:

Witold Sadowski, Wiktor Bartol

Tytuł:

Matematyka dla biologów

Autor:

Dariusz Wrzosek

Tytuł:

Matematyka dla programistów Java

Autor:

Jacek Piechota

Komentarze

Administrator

Data: 09-10-2017 20:56:23

Rzeczywiście moja pomyłka, tak to jest jak się rysuje dane z pamięci przeskakując z jednego okna programu na drugie :) Już poprawiłem

Aniia

Data: 09-10-2017 19:26:32

zad.4 błąd. W drzewku w drugiej urnie są pomylone wartości kul czarnych a białymi

Metematyka

Fizyka

Mechanika

Metrologia

Programowanie

Geometria

Obliczanie prawdopodobieństwa zdarzeń metodą drzewa

Komentarze

Administrator

Aniia