Wyznaczanie płaszczyzny ścięcia prostopadłośnianu płaszczyzną daną trzema punktami
Stronę tą wyświetlono już: 13412 razy
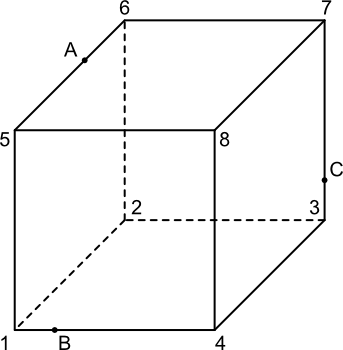
Dane są punkty A, B i C rozmieszczone na krawędziach prostopadłościanu jak na rysunku 1 zostało to pokazane. Pierwszą rzeczą, jaką należy zrobić z tymi nieszczęsnymi punktami to sprawdzić czy czasami dwa z nich nie przynależą do jednej płaszczyzny prostopadłościanu. Niestety w rozpatrywanym przypadku tak nie jest, przez co konieczne jest znalezienie punktu przebicia prostej przechodzącej przez wybraną parę punktów z jedną z płaszczyzn prostopadłościanu, na którym wiadomo, że jeden z punktów już leży.
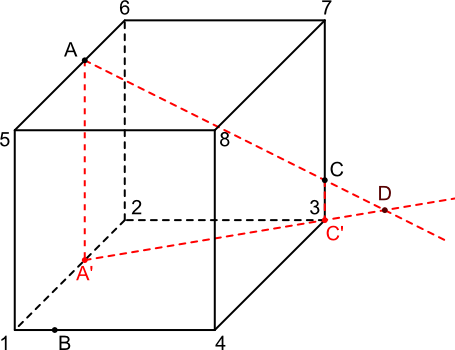
Czas zadać sobie konkretne pytanie i udzielić na nie równie konkretnej odpowiedzi, a pytanie to brzmi następująco: jak do diaska znaleźć punkt przebicia danej płaszczyzny prostą? Odpowiedź jest prostsza aniżeli by się wydawało, albowiem wystarczy jedynie znaleźć ślad naszej prostej na danej płaszczyźnie a jego punkt przecięcia się z prostą wyznaczy punkt przebicia.
Skoro zadane zostało już jedno ważne pytanie zagadka i została na nie udzielona równie ważna odpowiedź, czas czym prędzej podjąć życiową decyzję i wybrać parę punktów, dla których wyznaczyć należy punkt przebicia prostej przechodzącej przez nie z daną płaszczyzną. Ja wybrałem punkty A i C, tak by rzutować je na płaszczyznę podstawy, uzyskując tym samym punkty A', C', przez które przechodzi ślad linii zrzutowany na płaszczyznę podstawy 1-2-3-4. A dlaczegóż to wybrałem płaszczyznę 1-2-3-4 jako tą, na którą powinienem rzutować? Odpowiedź brzmi: bo na tej płaszczyźnie leży punkt B. A ktoś dociekliwy mógłby jeszcze zadać pytanie, dlaczego nie wybrałem płaszczyzny 1-4-8-5, na której również punkt B również leży? Odpowiedź brzmi: bo tak jest dla mnie wygodniej.
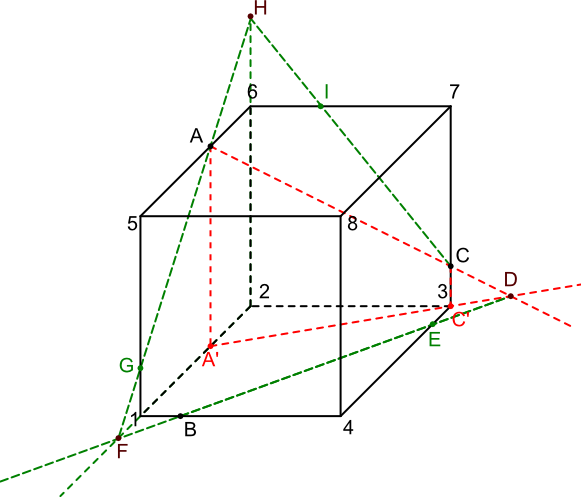
Punkt D przecięcia się śladu z prostą przechodzącą przez punkty A, C wyznacza drugi punkt, który leży w płaszczyźnie 1-2-3-4, teraz można połączyć ów punkt z punktem B, oznaczając punkt przecięcia się tejże linii z krawędzią 3-4 punktem E. Przedłużyć należy krawędź 1-2 oraz linię przechodzącą przez punkty B, E i D, otrzymując tym samym punkt F. Tenże punkt F należy do płaszczyzn: 1-2-3-4; 1-2-4-5 oraz (co ważniejsze) do płaszczyzny przechodzącej przez punkty A, B, C oraz parę innych, które wcześniej zostały już wyznaczone. Nie trudno jest zauważyć, że punkt F leży na tej samej płaszczyźnie co punkt A więc nie zwlekając już ani chwili, z najdzikszą rozkoszą połączmy te dwa punkty linią uzyskując dodatkowy punkt G przecięcia się jej z krawędzią 1-5 prostopadłościanu, ale, ale nie poprzestawajmy na tym, przedłużmy nowo powstałą linię oraz krawędź 2-6 znajdując tym samym punkt H. Mam nadzieję, że nie będzie wielkim zaskoczeniem stwierdzenie, że ów punkt H leży na płaszczyznach: 1-2-6-5, 2-3-7-6 oraz na płaszczyźnie ABC. Tak jakoś dziwnie się składa, że na płaszczyźnie 2-3-7-6 leży również punkt B. Nie zwlekajmy więc już ani chwili dłużej i połączmy punkt H i B prostą uzyskując w ten podstępny skądinąd sposób punkt I przecięcia się naszej prostej z krawędzią 6-7 prostopadłościanu. Po wykonaniu tych wszystkich jakże trudnych czynności nasz rysunek powinien wyglądać tak jak ten z poniższej ilustracji.
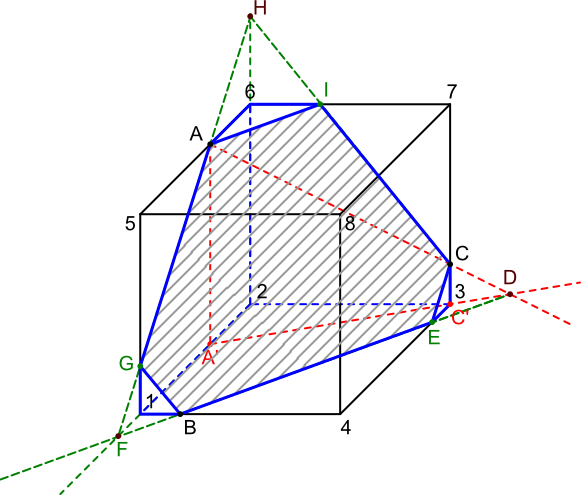
Cóż nam więc jeszcze do wykonania zostało? Łączymy punkty współpłaszczyznowe kolejno jak leci otrzymując płaszczyznę ścięcia C-E-B-G-A-I jak pokazane zostało to na rysunku 4
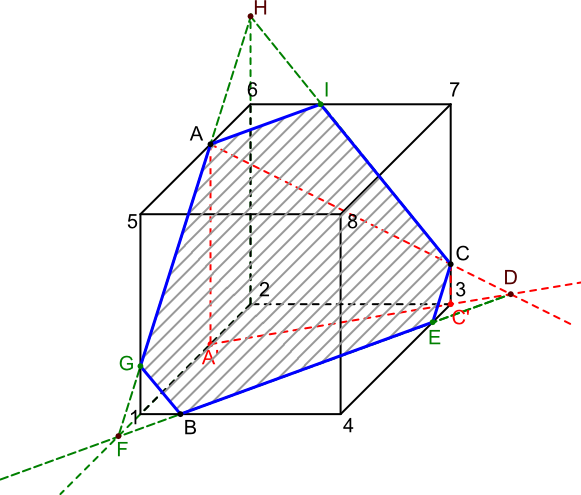
Na koniec zwykła uczciwość i przyzwoitość nakazuje, aby wybrać jedną część ściętej bryłki i ją pogrubić. Ja wybrałem tą część, która nie zasłania w tak mozolny sposób wyznaczonej płaszczyzny ścięcia uzyskując tym samym postać końcową jak na rysunku 5