Aksonometria
Stronę tą wyświetlono już: 25706 razy
Aksonometria to dział geometrii wykreślnej zajmujący się ilustracjami obiektów przestrzennych na płaskiej powierzchni z uwzględnieniem wszystkich trzech wymiarów na jednym rzucie. Możliwe jest to dzięki zastosowaniu układu osi, który w zasadzie może być dowolny jednak w technice stosuje się dwa podstawowe układy: izometryczny i ukośny.
Aksonometria izometryczna
W aksonometrii izometrycznej kąty pomiędzy poszczególnymi osiami są takie same i wynoszą 120° co zostało pokazane na rysunku 1. Dla takiego układu osi stosuje się jeden współczynnik skali e oraz współczynniki skrócenia wymiaru ex, ey oraz ez. Najczęściej współczynniki skrócenia przyjmuje się (z przyczyn praktycznych) jako równe 1.
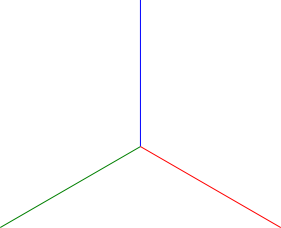
W tego typu układach okręgi przyjmują kształt eliptyczny, a ponieważ za pomocą standardowego cyrkla nie da się wykreślić elipsy więc stosuje się tutaj konstrukcję zastępczą jaką jest owal. Rysowanie owali zostało omówione w dziale: Geometria wykreślna → Podstawowe konstrukcje → Kreślenie owali
Aksonometria ukośna
Aksonometria ukośna ma dwie odmiany: kawalerską - gdzie oś x jest ustawiona poziomo (jak na rysunku 2) oraz wojskową - gdzie oś z jest ustawiona pionowo. W obu przypadkach pomiędzy osią x a osią y kąt jest równy 90° natomiast pomiędzy osią z a pozostałymi osiami kąt wynosi 135°. Dla wymiarów osi x oraz y współczynnik skrócenia w układzie kawalerskim może być różny od jedności jedynie dla osi y układu współrzędnych (najczęściej przyjmowany jako 1/2).
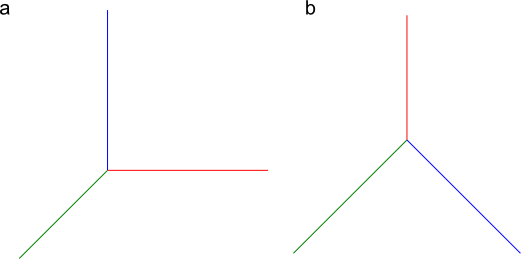
W aksonometrii wojskowej skróceniu ulega jedynie wymiar dla osi z, którego współczynnik skrócenia może przyjmować wartość 1/2.
W aksonometrii ukośnej okręgi rysowane na płaszczyźnie oxy zachowują swój naturalny kształt, dlatego też tak chętnie stosuje się je w ilustracjach zawierających dużą liczbę płaszczyzn lub otworów o kształcie okręgu, ponieważ upraszcza to rysowanie.
Odwzorowanie wymiarów w aksonometrii izometrycznej i ukośnej
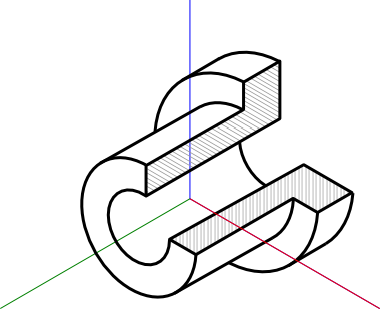
Na rysunku 3 pokazany został przykładowy obiekt narysowany w aksonometrii izometrycznej, gdzie okręgi nie zachowują swoich kształtów z powodu przyjętej perspektywy.
W przypadku aksonometrii ukośnej sprawy mają się nieco inaczej, a mianowicie okręgi leżące w płaszczyźnie xy zachowują swój pierwotny kształt (jak z resztą widać na rysunku 4.

