Perspektywa
Stronę tą wyświetlono już: 15983 razy
 | W tym dziale omówione zostały podstawy podstaw, aczkolwiek nadal wymaga on rozwinięcia |
Podstawowe definicje
Perspektywa jest pojęciem stosowanym w geometrii wykreślnej ale nie tylko bo również i w malarstwie oraz fotografii. W przypadku geometrii wykreślnej jest to takie rzutowanie danego obiektu na pewną płaszczyznę obserwacji, gdzie wszystkie punkty danego obiektu są rzutowane nie prostopadle do płaszczyzny obserwacji ale zbieżnie do punktu obserwatora O.
Dla lepszego zrozumienia tego, co powyżej napisałem zerknijmy łaskawym okiem na poniższy rysunek, gdzie widoczny jest punkt obserwatora O i płaszczyzna obserwacji. Na rysunku tym zaznaczona została najkrótsza odległość punktu obserwatora O od płaszczyzny obserwacji, którą jest promień δ. O znaczeniu promienia δ będę rozpisywał się w kolejnych podstronach tego poddziału, natomiast ważny jest jeszcze rzut punktu obserwatora Oτ na płaszczyznę obserwacji.
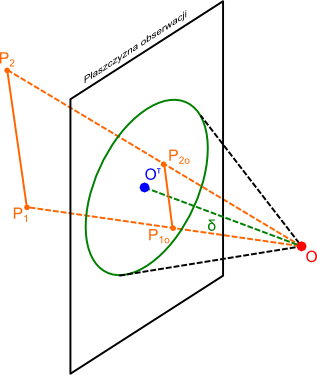
Oznaczania:
- O - punkt obserwatora;
- Oτ - rzut punktu obserwatora O na płaszczyznę obserwacji;
- δ - promień obserwacji;
- P1, P2 - punkty końcowe rzutowanego obiektu; P1o, P2o - punkty końcowe zrzutowanego obiektu na płaszczyznę obserwacji.
Rzutowanie punktów odcinka P1 - P2 na płaszczyznę obserwacji odbywa się poprzez znalezienie punktu przecięcia płaszczyzny obserwacji z linią łączącą punkt obserwacji O z danym końcem odcinka rzutowanego. W ten sposób znalezione zostały na rysunku 1 punkty zrzutowanego odcinka na płaszczyźnie obserwacji.
Podstawowe typy perspektywy
Istnieją trzy rodzaje perspektyw: z jednym punktem zbiegu (jednozbieżna); z dwoma punktami zbiegu (dwuzbieżna) i z trzema punktami zbiegu (trójzbieżna).
Perspektywa jednozbieżna
W tego typu perspektywie większość płaszczyzn obiektu jest ustawionych albo równolegle do płaszczyzny obserwacji, albo prostopadle do niej w wyniku czego: wszystkie płaszczyzny równoległe do płaszczyzny obserwacji zachowują swój kształt, natomiast zmienia się ich skala (wielkość) co wiąże się z oddaleniem obiektu obserwowanego od płaszczyzny obserwacji. Wszystkie linie prostopadłe do płaszczyzny obserwacji zbiegają się w jednym punkcie zbiegu Z.
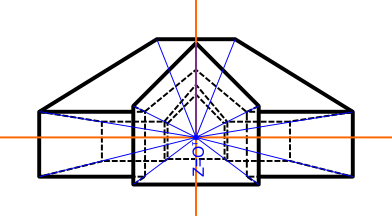
Perspektywa tego typu jest również nazywana perspektywą centralną, ponieważ obiekt rysowany w takiej perspektywie ma płaszczyzny umieszczone równolegle do płaszczyzny obserwacji.
Perspektywa dwuzbieżna
W tej perspektywie większość płaszczyzn obiektu jest ustawiona pod kątem względem płaszczyzny obserwacji, wynikiem czego na rysunku można wyróżnić dwie podstawowe grupy linii, które zbiegają się w jednym z dwóch punktów zbiegu Z1 lub Z2.
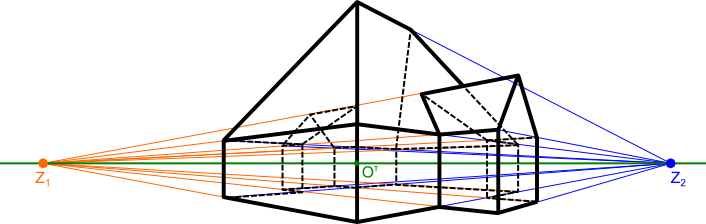
Na rysunku 3 zaznaczone zostały kolorami niebieskim i pomarańczowym dwie grupy linii zbiegu. Wspólną cechą wszystkich odcinków należących do tej samej grupy linii zbiegających się w jednym punkcie jest to, że w rzeczywistości są one równoległe, natomiast każda linia z grupy pierwszej jest w rzeczywistości prostopadła do każdej linii z grupy drugiej.
Perspektywa trójzbieżna
Perspektywa ta cechuje się (jak nie trudno się domyślić) aż trzema punktami zbieżności Z1, Z2 i Z3. Odcinki zbiegające się w jednym punkcie w rzeczywistości są do siebie równoległe. Odcinki z dwóch różnych punktów zbiegu są w rzeczywistości prostopadłe względem siebie.
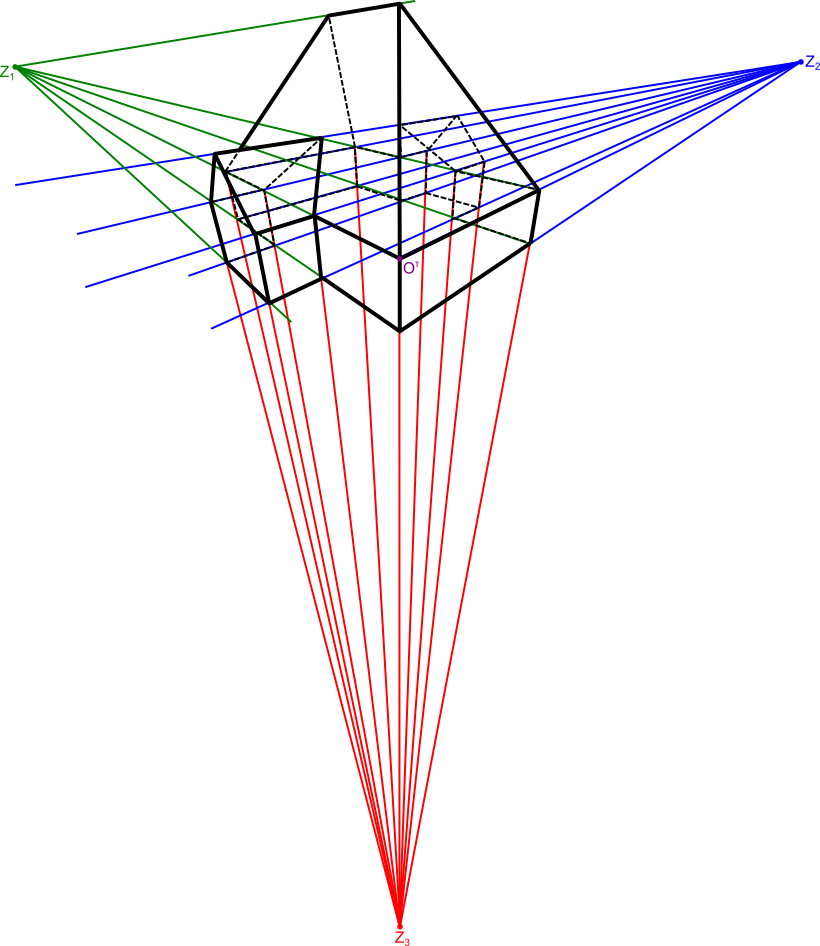
Powyżej wykreślona perspektywa jest najbardziej złożoną, ale i najlepiej oddającą rzeczywisty wygląd obiektów trójwymiarowych widzianych okiem człowieka czy też kamery lub aparatu.
