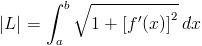Podstawowe wzory

Stronę tą wyświetlono już: 2712 razy

Wyznaczanie długości łuku funkcji f(x).

[1]

Zapis wyrażenia w formacie TeX-a:

|L|=\int_a^b\sqrt{1+\left[f'(x)\right]^2}\,dx

Przykład

Oblicz długość łuku funkcji

opisującej długość linii przekroju kadłuba statku w przedziale od -2 do 2.

Rozwiązanie:

Funkcja podcałkowa, która powstała po podstawieniu do wzoru [1] zadanej funkcji została już rozwiązana w dziale Matematyka: Całki oznaczone: Obliczanie całek z funkcji niewymiernych w zadaniu 14. Z tego względu w niniejszym miejscu nie rozpisuje się z opisem całego rozwiązania powstałej funkcji podcałkowej.

Wyznaczanie objętości bryły powstałej z obrotu figury zawartej między wykresem funkcji f(x) a osią x względem tejże osi.

[2]

Zapis wyrażenia w formacie TeX-a:

V=\pi\int_a^b\left[f(x)\right]^2\,dx

Przykład

Obliczyć pojemność naczynia, którego kształt wewnętrznej ścianki jest opisany następującą funkcją:

w przedziale od 0 do 4. Jako jednostkę przyjąć cm.

Rozwiązanie:

Wyznaczanie pola powierzchni powstałej z obrotu krzywej f(x) względem osi x.

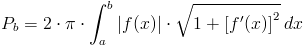[3]

Zapis wyrażenia w formacie TeX-a:

P_b=2\cdot\pi\cdot\int_a^b\left|f(x)\right|\cdot \sqrt{1+\left[f'(x)\right]^2}\,dx

Przykład

Obliczyć pole powierzchni wewnętrznej naczynia opisanej funkcją

w przedziale od 0 do 2, jako jednostkę obrać cm.

Rozwiązanie: