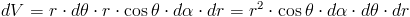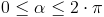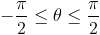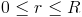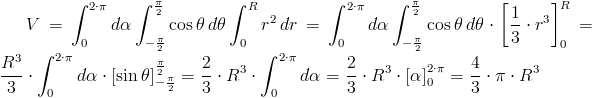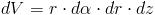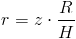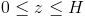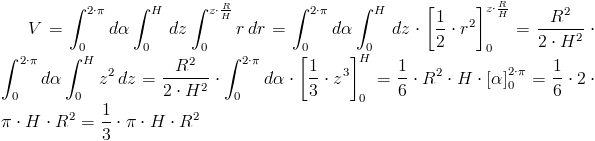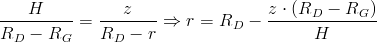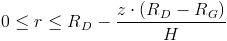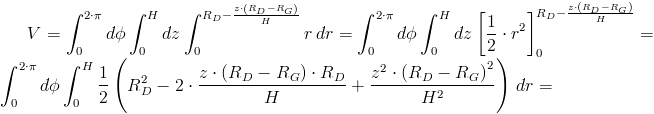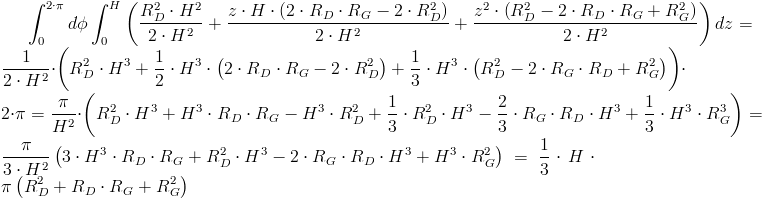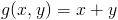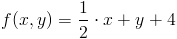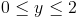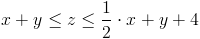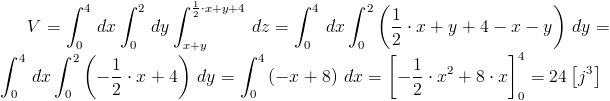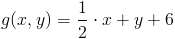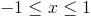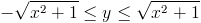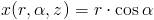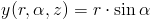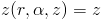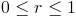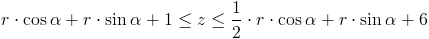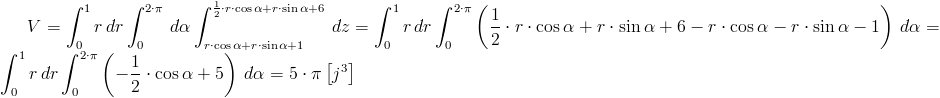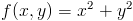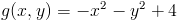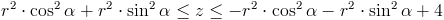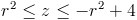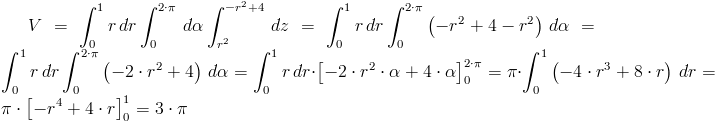Całki potrójne - obliczanie objętości

Stronę tą wyświetlono już: 2139 razy

Zadanie 1 Wyprowadzić wzór na objętość kuli.

Rysunek pomocniczy do kuli umożliwiający wyznaczenie wzoru na jej objętość
Rys. 1
Rysunek pomocniczy kuli z naniesionymi wielkościami fizycznymi.

Rozwiązanie:

Objętość elementarnego wycinka kuli dV można zapisać wzorem:

dV=rcdot dthetacdot rcdotcosthetacdot dalphacdot dr=r^2cdotcosthetacdot dalphacdot dtheta cdot dr

gdzie:

  • r⋅dθ - długość elementarnego wycinka kuli;
  • r⋅cosθ⋅dα - szerokość elementarnego wycinka kuli;
  • dr - wysokość elementarnego wycinka kuli.

Granice całkowania:

0lealphale2cdotpi

-frac{pi}{2}le hetalefrac{pi}{2}

0le rle R

Wyznaczenie wzoru na objętość V kuli:

V=int_0^{2cdotpi}dalphaint_{-frac{pi}{2}}^frac{pi}{2}costheta,dthetaint_0^Rr^2,dr=int_0^{2cdotpi}dalphaint_{-frac{pi}{2}}^frac{pi}{2}costheta,dthetacdotleft[frac{1}{3}cdot r^3right]_0^R=frac{R^3}{3}cdotint_0^{2cdotpi}dalphacdotleft[sinthetaright]_{-frac{pi}{2}}^frac{pi}{2}=frac{2}{3}cdot R^3cdotint_0^{2cdotpi}dalpha=frac{2}{3}cdot R^3cdotleft[alpharight]_0^{2cdotpi}=frac{4}{3}cdotpicdot R^3

Zadanie 2 Wyznaczyć wzór na objętość stożka o podanej wysokości H i promieniu podstawy R.

Rysunek pomocniczy do zadania 2
Rys. 2
Rysunek pomocniczy stożka z naniesionymi wielkościami fizycznymi.

Rozwiązanie:

Elementarna objętość dV:

dV=rcdot dalphacdot drcdot dz

gdzie:

  • r⋅dα - szerokość elementarnego wycinka stożka;
  • dr - długość elementarnego wycinka stożka;
  • dz - wysokość elementarnego wycinka stożka.

Zależność promienia r od jego położenia na osi z oraz wysokości H i promienia podstawy R stożka:

r=zcdot frac{R}{H}

Granice całkowania:

0lealphale 2cdotpi

0le zle H

0le rle zcdot frac{R}{H}

Wyprowadzenie wzoru na objętość V stożka:

V=int_0^{2cdotpi}dalpha int_0^H,dzint_0^{zcdotfrac{R}{H}}r,dr=int_0^{2cdotpi}dalpha int_0^H,dzcdotleft[frac{1}{2}cdot r^2 ight]_0^{zcdotfrac{R}{H}}=frac{R^2}{2cdot H^2}cdotint_0^{2cdotpi}dalphaint_0^Hz^2,dz=frac{R^2}{2cdot H^2}cdotint_0^{2cdotpi}dalphacdotleft[frac{1}{3}cdot z^3 ight]_0^H=frac{1}{6}cdot R^2cdot Hcdotleft[alpha ight]_0^{2cdotpi}=frac{1}{6}cdot 2cdot picdot Hcdot R^2=frac{1}{3}cdotpicdot Hcdot R^2

Zadanie 3 Wyznaczyć wzór na objętość stożka ściętego o danej wysokości H i promieniach RD, RG.

Rysunek pomocniczy do zadania 3
Rys. 3
Rysunek pomocniczy stożka ściętego z naniesionymi wielkościami fizycznymi.

Rozwiązanie:

Objętość dV elementarnego wycinka stożka ściętego:

dV=rcdot dalphacdot drcdot dz

Zależność promienia r od jego położenia na osi z oraz od wysokości H i promieni RD, RD stożka ściętego:

frac{H}{R_D-R_G}=frac{z}{R_D-r}Rightarrow r = R_D-frac{zcdot left(R_D-R_G ight)}{H}

Granice całkowania:

0lealphale2cdotpi

0le zle H

0le rle R_D-frac{zcdot left(R_D-R_G ight)}{H}

Wyprowadzenie wzoru na objętość V stożka ściętego:

V=int_0^{2cdot pi}dphi int_0^Hdzint_0^{R_D-frac{zcdot left(R_D-R_G ight)}{H}}r, dr=int_0^{2cdot pi}dphiint_0^Hdzleft[frac{1}{2}cdot r^2 ight]_0^{R_D-frac{zcdot left(R_D-R_G ight)}{H}}=int_0^{2cdot pi}dphi int_0^Hfrac{1}{2}left(R_D^2-2cdot frac{zcdot left(R_D-R_G ight)cdot R_D}{H}+frac{z^2cdot left(R_D-R_G ight)^2}{H^2} ight), dr=

int_0^{2cdot pi}dphi int_0^Hleft(frac{R_D^2cdot H^2}{2cdot H^2}+frac{zcdot Hcdot left(2cdot R_Dcdot R_G-2cdot R_D^2 ight)}{2cdot H^2}+frac{z^2cdot left(R_D^2-2cdot R_Dcdot R_G+ R_G^2 ight)}{2cdot H^2} ight)dz=frac{1}{2cdot H^2}cdot left(R_D^2cdot H^3+frac{1}{2}cdot H^3cdot left(2cdot R_Dcdot R_G-2cdot R_D^2 ight)+frac{1}{3}cdot H^3cdotleft(R_D^2-2cdot R_Gcdot R_D+R_G^2 ight) ight)cdot 2cdot pi=frac{pi}{H^2}cdot left(R_D^2cdot H^3+H^3cdot R_Dcdot R_G-H^3cdot R_D^2+frac{1}{3}cdot R_D^2cdot H^3-frac{2}{3}cdot R_Gcdot R_Dcdot H^3+frac{1}{3}cdot H^3cdot R_G^3 ight)=frac{pi}{3cdot H^2}left(3cdot H^3cdot R_Dcdot R_G+R_D^2cdot H^3-2cdot R_Gcdot R_Dcdot H^3+H^3cdot R_G^2 ight)=frac{1}{3}cdot Hcdotpileft(R_D^2+R_Dcdot R_G+R_G^2 ight)

Zadanie 4 Obliczyć objętość bryły ograniczonej od dołu funkcją:

g(x,y)=x+y

zaś od góry funkcją:

f(x,y)=frac{1}{2}cdot x+y+4

nad obszarem całkowania 0≤x≤4 oraz 0≤y≤2.

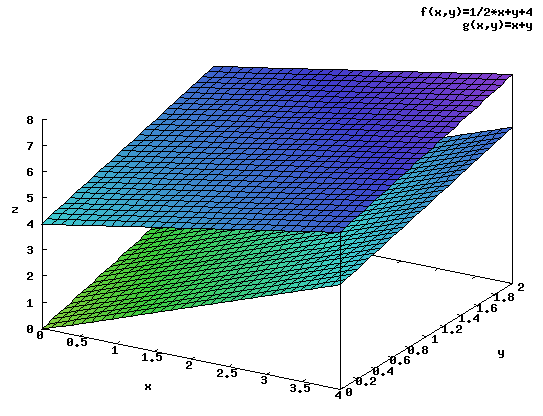
Wykres funkcji <b>f(x,y)</b>, <b>g(x,y)</b> w przedziale całkowania.
Rys. 4
Wykres funkcji f(x,y), g(x,y) w przedziale całkowania.

Rozwiązanie:

Przedziały całkowania:

0le x le4

0le y le2

x+yle zlefrac{1}{2}cdot x+y+4

Obliczenie objętości V:

V=int_0^4,dxint_0^2,dyint_{x+y}^{frac{1}{2}cdot x+y+4},dz=int_0^4,dxint_0^2left(frac{1}{2}cdot x+y+4-x-y ight), dy=int_0^4,dxint_0^2left(-frac{1}{2}cdot x+4 ight),dy=int_0^4left(-x + 8 ight),dx=left[-frac{1}{2}cdot x^2+8cdot x ight]_0^4=24left[j^3 ight]

Zadanie 5 Obliczyć objętość walca o promieniu R=1 ściętego od dołu funkcją:

f(x,y)=x+y+1

zaś od góry funkcją:

g(x,y)=frac{1}{2}cdot x+y+6

Przedziały całkowania w współrzędnych kartezjańskich:

-1le xle 1

-sqrt{x^2+1}le y lesqrt{x^2+1}

x+y+1le zle frac{1}{2}cdot x+y+6

Jak widać nie zanosi się na łatwe obliczenia, chyba że zamieni się współrzędne kartezjańskie na walcowe. W tym celu warto zapisać zależność funkcyjną współrzędnych x, y, z od współrzędnych walcowych r, α, z:

x(r,alpha,z)=rcdotcosalpha

y(r,alpha,z)=rcdotsinalpha

z(r,alpha,z)=z

Ogólny wzór na jakobian przekształcenia:

Równanie [1] [1]

Zapis wyrażenia w formacie TeX-a:

J(u,v,w)=\begin{vmatrix} c\frac{\partial x}{\partial u} && \cfrac{\partial x}{\partial v} & \cfrac{\partial x}{\partial w}\\ \cfrac{\partial y}{\partial u} && \cfrac{partial y}{partial v} & cfrac{partial y}{partial w}\\ \cfrac{\partial z}{\partial u} & \cfrac{\partial z}{\partial v} & \cfrac{\partial z}{\partial w} \end{vmatrix}

W tym przypadku u=r, v=α, w=z, w związku z czym jakobian dla współrzędnych walcowych przyjmuje następującą postać:

Równanie [2] [2]

Zapis wyrażenia w formacie TeX-a:

J(r,alpha,z)=\begin{vmatrix}\cfrac{\partial x}{\partial r} && \cfrac{\partial x}{\partial \alpha} && \cfrac{\partial x}{\partial z}\\ \cfrac{\partial y}{\partial r} && \cfrac{\partial y}{\partial \alpha} && \cfrac{\partial y}{\partial z}\\ \cfrac{\partial z}{\partial r} && \cfrac{\partial z}{\partial \alpha} && \cfrac{\partial z}{\partial z}\end{vmatrix}=\begin{vmatrix} \cos\alpha && -rcdotsinalpha && 0\\ \sin\alpha && r\cdot\cos\alpha && 0\\ 0 && 0 && 1 \end{vmatrix}=r\cdot\cos^2\alpha+r\cdot\sin^2\alpha=r

Wzór na zamianę całki w jednym układzie współrzędnych na całkę w drugim układzie współrzędnych:

Równanie [3] [3]

Zapis wyrażenia w formacie TeX-a:

intintint_Omega f(x,y,z),dx,dy,dz=intintint_U f(u,v,w)cdot J(u,v,w),du,dv,dw

w tym przypadku funkcja gęstości nas nie interesuje tylko objętość V ściętego walca więc wartość owej funkcji musi się równać 1 a co za tym idzie również funkcja f(u,v,w)=1.

Przedziały całkowania w układzie współrzędnych sferycznych:

0le rle 1

0le alphale 2cdotpi

x+y+1le zle frac{1}{2}cdot x+y+6

W ostatnim przedziale całkowania dla zmiennej z należy podstawić za x funkcję x(r, α, z), za y funkcję x(r, α, z):

rcdotcosalpha+rcdotsinalpha+1le zle frac{1}{2}cdot rcdotcosalpha+rcdotsinalpha+6

Rozwiązanie:

V=int_0^1r,drint_0^{2cdotpi},dalphaint_{rcdotcosalpha+rcdotsinalpha+1}^{frac{1}{2}cdot rcdotcosalpha+rcdotsinalpha+6},dz=int_0^1r,drint_0^{2cdotpi}left(frac{1}{2}cdot rcdotcosalpha+rcdotsinalpha+6-rcdotcosalpha-rcdotsinalpha-right),dalpha=int_0^1r,drint_0^{2cdotpi}left(-frac{1}{2}cdotcosalpha+5right),dalpha=5cdotpileft[j^3right]

Zadanie 6 Obliczyć objętość walca o promieniu R=1 ściętego od dołu funkcją:

f(x,y)=x^2+y^2

zaś od góry funkcją:

g(x,y)=-x^2-y^2+4

Na rysunku 5 można obejrzeć wykres funkcji g(x,y), f(x,y).

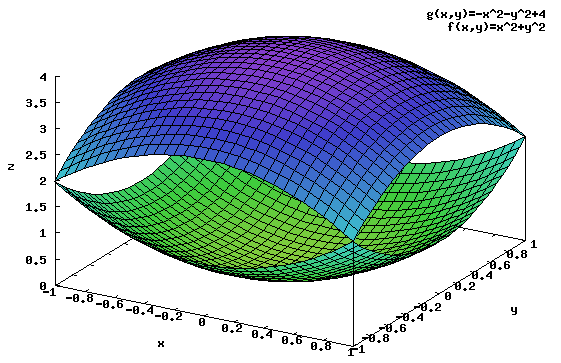
Wykres funkcji <b>f(x,y)</b>, <b>g(x,y)</b>.
Rys. 5
Wykres funkcji f(x,y), g(x,y).

Rozwiązanie:

Przedziały całkowania we współrzędnych walcowych:

0le rle 1

0le alphale 2cdotpi

r^2cdotcos^2alpha+r^2cdotsin^2alphale zle -r^2cdotcos^2alpha-r^2cdotsin^2alpha+4

Po uproszczeniu granic całkowania dla zmiennej z:

r^2le zle -r^2+4

Obliczenie objętości V:

V=int_0^1r,drint_0^{2cdotpi},dalphaint_{r^2}^{-r^2+4},dz=int_0^1r,drint_0^{2cdotpi}left(-r^2+4-r^2 ight),dalpha=int_0^1r,drint_0^{2cdotpi}left(-2cdot r^2+4 ight),dalpha=int_0^1r,drcdotleft[-2cdot r^2cdotalpha+4cdotalpha ight]_0^{2cdotpi}=picdotint_0^1left(-4cdot r^3+8cdot r ight),dr=picdotleft[-r^4+4cdot r ight]_0^1=3cdotpi

Komentarze