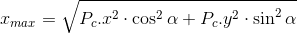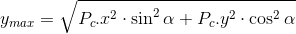Obliczanie granic obszaru prostokątnego obróconej elipsy
Stronę tą wyświetlono już: 2185 razy
Gdy dana jest elipsa opisana następującymi parametrami:
- rx - promień na osi x;
- ry - promień na osi y;
- xc i yc - współrzędne środka elipsy;
- α - kąt obrotu elipsy
wtedy możliwe jest obliczenie prostokąta, w który ta elipsa się wpisuje, a którego boki są równoległe do osi x i y jak pokazane zostało to na rysunku poniżej.
Najprościej rzecz ujmując, aby obliczyć xmax i ymax konieczne jest znalezienie stycznej do elipsy, której kąt będzie równy 0, czyli dla której pochodna w danym punkcie jest równa zero. Oto gotowe wzory na xmax i ymax:

Tytuł:
Algorytmy. Ilustrowany przewodnik
Autor:
Aditya Bhargava

Tytuł:
Algorytmy. Struktury danych i złożoność obliczeniowa
Autor:
Feliks Kurp

Tytuł:
Algorytmy w Pythonie. Techniki programowania dla praktyków
Autor:
Piotr Wróblewski

Tytuł:
Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie
Autor:
Ryan T. White, Archana Tikayat Ray

Tytuł:
Algorytmy kryptograficzne w Pythonie. Wprowadzenie
Autor:
Shannon W. Bray

Tytuł:
Algorytmy sztucznej inteligencji. Ilustrowany przewodnik
Autor:
Rishal Hurbans

Tytuł:
Algorytmy bez tajemnic
Autor:
Thomas H. Cormen

Tytuł:
Algorytmy dla bystrzaków
Autor:
John Paul Mueller, Luca Massaron

Tytuł:
Algorytmy Data Science. Siedmiodniowy przewodnik. Wydanie II
Autor:
David Natingga

Tytuł:
Algorytmy uczenia maszynowego. Zaawansowane techniki implementacji
Autor:
Giuseppe Bonaccorso