Doświadczenie losowe, zbiór jego wyników, zdarzenie losowe oraz zdarzenie elementarne
Stronę tą wyświetlono już: 6631 razy
Doświadczeniem losowym jest doświadczenie, które może być dowolnie powtarzane w warunkach identycznych lub zbliżonych, a którego wyniku nie da się jednoznacznie przewidzieć.
Zbór wszystkich wyników danego doświadczenia nazywa się zbiorem (przestrzenią) wszystkich zdarzeń elementarnych i oznacza się go symbolem Ω (czyt. omega).
Pojedynczy element zdarzenia nazywa się zdarzeniem elementarnym i oznacza się je symbolem ω z indeksem dolnym np. ω1, ω2, ..., ωn.
Przykład
Ze zbioru A={1; 2; 4; 7} losujemy ze zwracaniem dwie cyfry budując liczbę dwucyfrową. Ile istnieje możliwych wyników takiego losowania.
Uwaga!
1) Doświadczenie jednoetapowe - jedno losowanie, jeden wybór lub też jedna próba (wszystkich wyników takiego doświadczenia jest tyle, ile zbiór A zawiera elementów.
Doświadczenie wieloetapowe - polega na powtarzaniu jednej próby n razy.
Rozwiązanie:
W tym przypadku mamy do czynienia z doświadczeniem dwuetapowym, tworzę więc dwuetapowe wariacje z powtórzeniami ze zbioru czteroelementowego.
Zbiór Ω składa się z 16-tu zdarzeń elementarnych. Pojedynczym zbiorem elementarnym jest utworzona liczba dwucyfrowa.
Ω={22; 32; 52; 72; 23; 33; 53; 73; 25; 35; 55; 75; 27; 35; 55; 75; 27; 37; 57; 77}
Dowolny podzbiór zbioru wszystkich zdarzeń elementarnych Ω nazywamy zdarzeniem losowym (lub krócej zdarzeniem) i oznaczamy dużymi literami A, B, C ... itd.
A - zdarzenie, w którym utworzona liczba dwucyfrowa jest parzysta.
A = {22; 32; 52; 72}
Liczebność zbioru A jest równa 4
Uwaga!
ω = A - czyta się: "zdarzenie elementarne ω sprzyja zajściu zdarzenia losowego A
ω ≠ A - czyta się: "zdarzenie elementarne ω nie sprzyja zajściu zdarzenia losowego A
Zapis 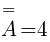 czytamy: "zdarzeniu losowemu A sprzyjają cztery zdarzenia elementarne
czytamy: "zdarzeniu losowemu A sprzyjają cztery zdarzenia elementarne
Zdarzeniu losowemu B nie sprzyja żadna z otrzymanych liczb dwucyfrowych. 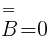 .
.
Jeżeli danemu zdarzeniu losowemu nie sprzyja żadne zdarzenie elementarne, to takie zdarzenie nazywa się niemożliwym i oznacza przez ϕ, tzn. 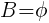
C - zdarzenie, w którym dana liczba jest większa niż 21
Zdarzenie C jest zdarzeniem pewnym ponieważ jest on równy zbiorowi Ω, co oznacza, że zdarzeniu C sprzyjają wszystkie zdarzenia elementarne danego doświadczenia.
Zadanie 1
Z talii 52 kart losowo wybrano trzy karty: a) określ i oblicz zbiór wszystkich możliwych zdarzeń elementarnych; b) oblicz liczbę zdarzeń elementarnych sprzyjających zajściu zdarzeń: A - zdarzenie, w którym wylosowano jednego asa; B zdarzenie, w którym wylosowano same asy; C zdarzenie, w którym nie wylosowano żadnego asa.
Rozwiązanie
a) Doświadczenie trój-etapowe.
Zbiór Ω tworzy trój-etapowe kombinacje bez powtórzeń ze zbioru 52-elementowego.
Zbiór Ω składa się z 22100 elementów. Inaczej można zapisać 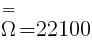
b) liczebność zbioru zdarzeń A obliczymy z iloczynu dwóch kombinacji bez powtórzeń w następujący sposób:
![Równanie [3]](https://obliczeniowo.com.pl/rownania/w_2449.gif) | [3] |
Zapis wyrażenia w formacie TeX-a:
Liczebność zbioru B obliczymy z kombinacji bez powtórzeń dla n=4 bo w talii znajdują się tylko cztery asy (no chyba, że ktoś oszukuje).
Liczebność zbioru C obliczymy z kombinacji bez powtórzeń dla n=48, bo tyle ma talia pozbawiona w bestialski sposób asów.
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_2451.gif) | [5] |
Zapis wyrażenia w formacie TeX-a:
Zadanie 2
Wykonujemy czterokrotny rzut monetą: a) opisz zbiór Ω; b) wypisz i oblicz zdarzenia elementarne sprzyjające zdarzeniu: A zdarzenie, w którym wypadły same reszki; B - zdarzenie, w którym wypadły dokładnie dwie reszki; C - zdarzenie, w którym wypadła co najwyżej jedna reszka.
Rozwiązanie:
a) Zbiór Ω tworzą cztero-elementowe wariacje z powtórzeniami ze zbioru dwu-elementowego (doświadczenie cztero-etapowe).
Zbiór Ω={(O; O; O; O) (O; O; O; R) (O; O; R; O) (O; O; R; R) (O; R; O; O) (O; R; O; R) (O; R; R; R;) (R; O; O; O) (R; O; O; R) (R; O; R; O) (R; O; R; R) (R; R; O; O) (R; R; O; R) (R; R; R; O) (R; R; R; R)}
b) Zbiór A={(R; R; R; R)}, liczebność jego wynosi 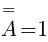
Zbiór B={(R;R;O;O} (R;O;R;O) (O; R; O; R) (O; O; R; R) (O; R; R; O) (R; O; O; R)}, liczebność jego wynosi 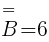
Zbiór C={(O; O; O; O) (O; O; O; R) (O; O; R; O) (O; R; O; O); (R; O; O; O)}, liczebność tego zbiory wynosi 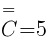

Tytuł:
Matematyka w uczeniu maszynowym
Autor:
Marc Peter Deisenroth, A. Aldo Faisal, Cheng Soon Ong

Tytuł:
Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie
Autor:
Ryan T. White, Archana Tikayat Ray

Tytuł:
Matematyka w Pythonie. Algebra, statystyka, analiza matematyczna i inne dziedziny
Autor:
Amit Saha

Tytuł:
Matematyka dla menedżerów. Wydanie II
Autor:
Michael C. Thomsett

Tytuł:
Matematyka Poradnik encyklopedyczny
Autor:
I.N. Bronsztejn, K.A. Siemiendiajew

Tytuł:
Matematyka finansowa
Autor:
Jacek Jakubowski, Andrzej Palczewski, Marek Rutkowski, Łukasz Stettner

Tytuł:
Proste jak pi Matematyka to bułka z masłem
Autor:
Liz Strachan

Tytuł:
O twierdzeniach i hipotezach. Matematyka według Delty
Autor:
Witold Sadowski, Wiktor Bartol

Tytuł:
Matematyka dla biologów
Autor:
Dariusz Wrzosek

Tytuł:
Matematyka dla programistów Java
Autor:
Jacek Piechota

![Równanie [1]](https://obliczeniowo.com.pl/rownania/w_2447.gif)
![Równanie [2]](https://obliczeniowo.com.pl/rownania/w_2448.gif)
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_2450.gif)
![Równanie [6]](https://obliczeniowo.com.pl/rownania/w_2452.gif)