Autor podstrony: Krzysztof Zajączkowski

Stronę tą wyświetlono już: 4148 razy

Na wcześniejszych stronach działu Geometria wykreślna → Perspektywa omówione zostały już metody kreślenia obiektów z uwzględnieniem perspektywy jednozbieżnej oraz dwuzbieżnej. Nie będzie więc złamaniem wielkiej tajemnicy, gdy napiszę, że nadeszła pora na omówienie kreślenia obiektów w perspektywie trójzbieżnej.

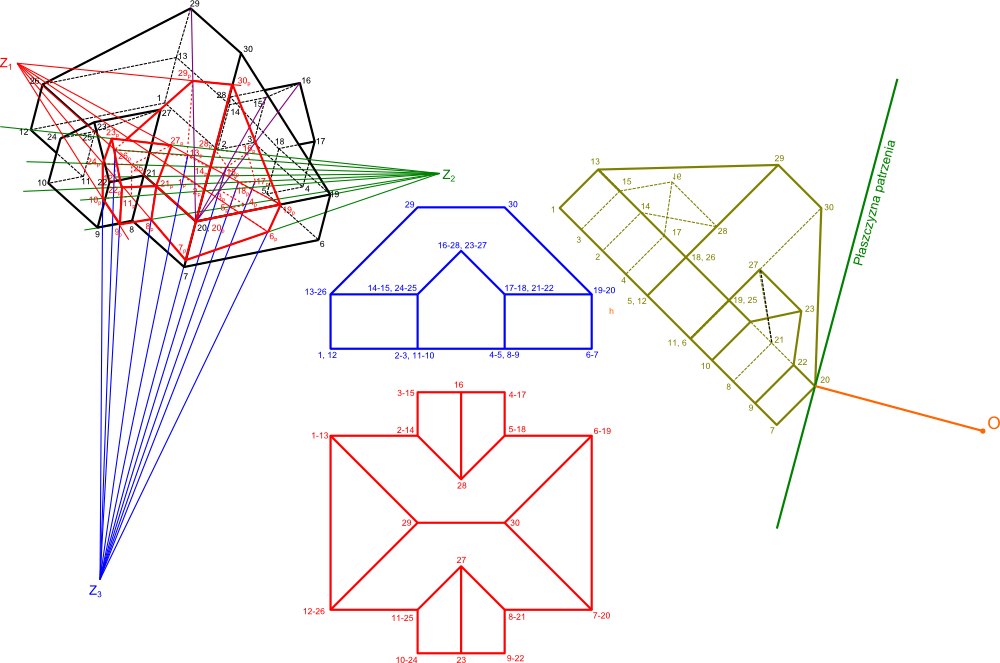
Przykład perspektywy trójzbierzniej otrzymanej na podstawie wejściowych dwóch rzutów prostopadłych oraz dwóch pochodnych rzutów, które umożliwiły wykreślenie danego obiektu w perspektywie metodą z definicji.
Rys. 1
Przykład perspektywy trójzbierzniej otrzymanej na podstawie wejściowych dwóch rzutów prostopadłych oraz dwóch pochodnych rzutów, które umożliwiły wykreślenie danego obiektu w perspektywie metodą z definicji.

Opis oznaczeń:

  • 1, 2 ... - punkty bocznego rzutu obiektu;
  • 1, 2 ... - punkty górnego rzutu obiektu;
  • 1, 2 ... - punkty rzutu bocznego pod kątem 45° względem ścian bocznych;
  • 1, 2 ... - punkty rzutu skośnego ustawionego pod kątem 60° względem podstawy obiektu;
  • 1p, 2p, ... - punkty rzutu obiektu na płaszczyznę obserwacji;
  • O - punkt patrzenia;
  • Z1, Z2, Z3 - punkty zbiegu

Na rysunku 1 obraz obiektu w perspektywie został uzyskany poprzez zastosowanie rzutowania metodą z definicji, która z kolei została dokładniej omówiona na stronie Geometria wykreślna → Perspektywa → Perspektywa jednozbieżna - metoda kreślenia z definicji. Kluczowe w powyższym rozwiązaniu jest samo ustawienie rzutów jak i płaszczyzny patrzenia, które mają wpływ na rodzaj uzyskanej perspektywy.

Punkty zbiegu Z1, Z2, Z3 można wyznaczyć poprzez znalezienie położenia w perspektywie co najmniej dwóch odcinków dla każdego z trzech podstawowych grup będących względem siebie prostopadłymi.

Tematy powiązane