Perspektywa dwuzbieżna
Stronę tą wyświetlono już: 7980 razy
Na łamach wcześniejszych stron tego działu opisywana już była technika pozyskiwania perspektywy jednozbieżnej zarazem metodą związaną bezpośrednio z definicją perspektywy jak i metodą związaną z zastosowaniem punktów głębi G. W tamtych przypadkach większość ścian obiektu była rozmieszczona względem płaszczyzny patrzenia pod kątem prostopadłym lub równoległym. Tym razem jednak płaszczyzna patrzenia zostanie umieszczona pod kątem różnym niż 90° lub 0° względem ścian obserwowanego obiektu wynikiem czego główne jego płaszczyzny oraz ich krawędzie będą zbiegały się w dwóch punktach zbiegu Z1 i Z2.
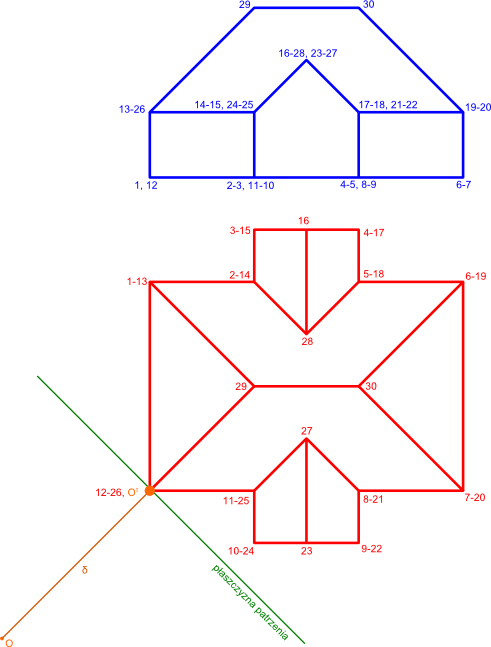
Opis oznaczeń:
- Oτ - rzut punktu obserwatora O na powierzchnię obserwacji
- O - punkt obserwacji;
- δ - promień obserwacji;
- 1, 2, ... - punkty obiektu na rzucie prostopadłym dolnym;
- 1, 2, ... - punkty obiektu na rzucie prostopadłym górnym.
Niestety, tym razem płaszczyzna patrzenia jest umieszczona pod kątem więc trzeba koniecznie wykorzystać wiedzę zdobytą w dziale Geometria wykreślna → Rzuty Monge'a, aby uzyskać prostokątny rzut danego obiektu w płaszczyźnie równoległej do płaszczyzny obserwacji, co też i uczyniłem na rysunku poniższym.
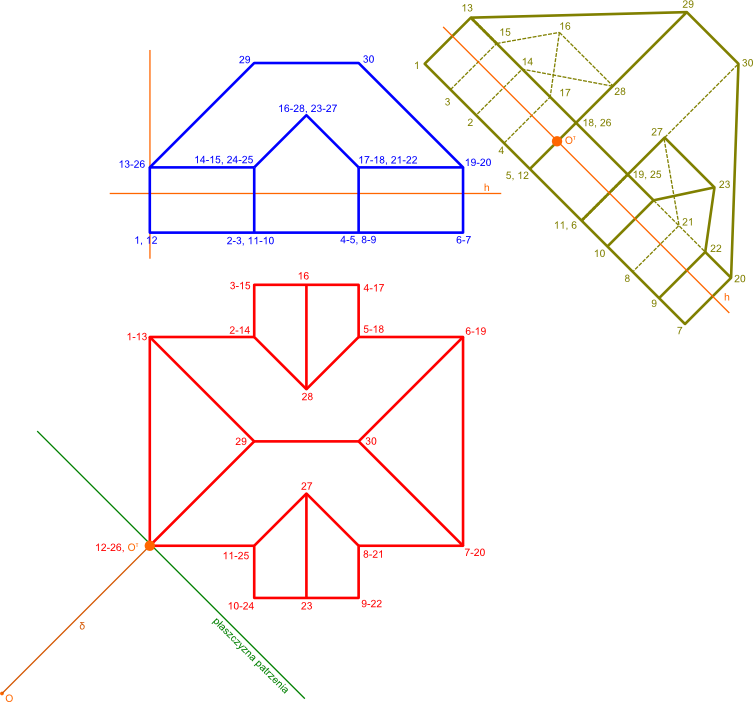
Opis oznaczeń:
- Oτ - rzut punktu obserwatora O na powierzchnię obserwacji
- O - punkt obserwacji;
- δ - promień obserwacji;
- 1, 2, ... - punkty obiektu na rzucie prostopadłym dolnym;
- 1, 2, ... - punkty obiektu na rzucie prostopadłym górnym.
- 1, 2, ... - punkty obiektu na dodatkowym rzucie prostokątnym.
Drodzy Czytelnicy, bądźmy rozsądnymi ludźmi i dla uproszczenia sprawy zapomnijmy o niebieskim, górnym rzucie prostokątnym a skupmy swą uwagę na pozostałych rzutach. Dla uproszczenia sprawy rysunek 2 zastępuję poniższym rysunkiem 3.
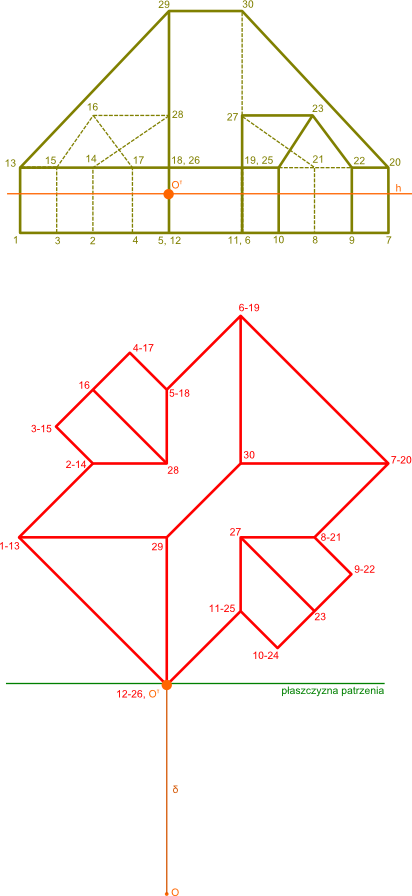
Opis oznaczeń:
- Oτ - rzut punktu obserwatora O na powierzchnię obserwacji
- O - punkt obserwacji;
- δ - promień obserwacji;
- 1, 2, ... - punkty obiektu na rzucie prostopadłym górnym.
- 1, 2, ... - punkty obiektu na dodatkowym rzucie prostokątnym.
Wykorzystując nabytą wcześniej wiedzę z odnajdywania punktów w perspektywie jednozbieżnej można a nawet trzeba znaleźć rzuty punktów naszego obiektu na płaszczyznę obserwacji, jedyną różnicą będzie tutaj fakt, że większość linii krawędzi obiektu będzie zbiegała się albo w punkcie zbiegu Z1, albo w punkcie zbiegu Z2.
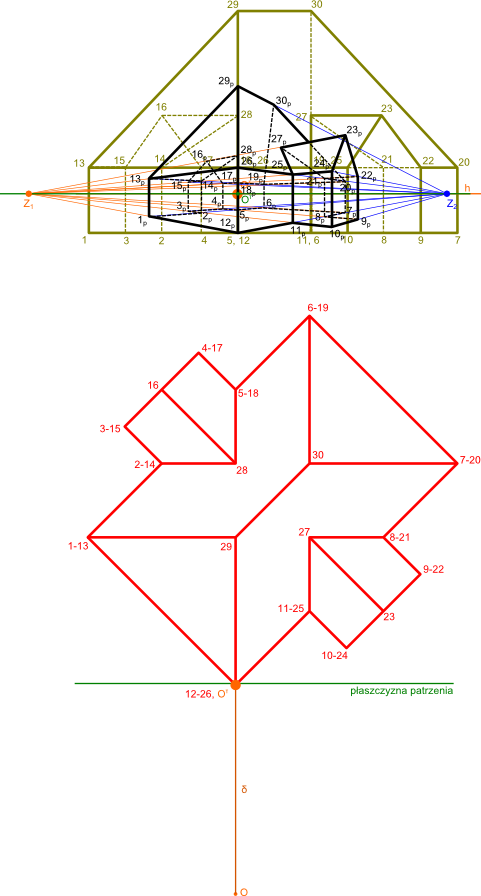
Opis oznaczeń:
- Oτ - rzut punktu obserwatora O na powierzchnię obserwacji
- O - punkt obserwacji;
- δ - promień obserwacji;
- 1, 2, ... - punkty obiektu na rzucie prostopadłym górnym.
- 1, 2, ... - punkty obiektu na dodatkowym rzucie prostokątnym.
- 1p, 2p, ... - rzut obiektu w perspektywie.
Sam obiekt w pewnym powiększeniu będzie wyglądał tak jak na poniższym rysunku.
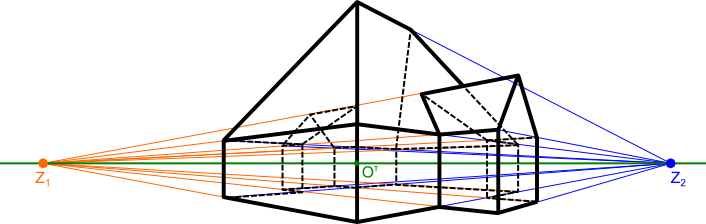
Opis oznaczeń:
- Oτ - rzut punktu obserwatora O na powierzchnię obserwacji
- Z1, Z2 - punkty zbiegu krawędzi obiektu.
