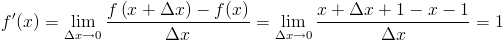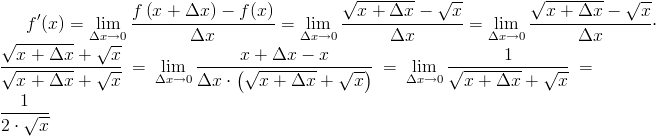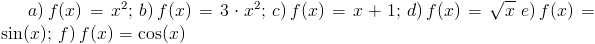Obliczenia pochodnych funkcji z definicji
Podstawowe wzory
Obliczenia pochodnych funkcji z definicji
Podstawowe twierdzenia o pochodnych funkcji
Zadania
Wzór prostej stycznej do funkcji
Ta strona należy do działu:
poddziału
Autor podstrony: Krzysztof Zajączkowski
Stronę tą wyświetlono już: 14567 razy
Obliczyć za pomocą wzoru [2] z działu Matematyka → Pochodna funkcji pochodne następujących funkcji:
Pochodna funkcji a :
Zapis wyrażenia w formacie TeX-a:
f'(x)=\lim_{\Delta x\rightarrow 0}\frac{f\left(x+\Delta\right) -f(x)}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{\left(x+\Delta x\right)^2-x^2}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{x^2+2\cdot x\cdot\Delta x+\Delta x^2-x^2}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{2\cdot x\cdot\Delta x+\Delta x^2}{\Delta x}=\lim_{\Delta x\rightarrow 0}2\cdot x+\Delta x=2\cdot x
Pochodna funkcji b :
Zapis wyrażenia w formacie TeX-a:
f'(x)=\lim_{\Delta x\rightarrow 0}\frac{f\left(x+\Delta\right) -f(x)}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{3\cdot\left(x+\Delta x\right)^2-3\cdot x^2}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{3\cdot x^2+6\cdot x\cdot\Delta x+3\cdot \Delta x^2-3\cdot x^2}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{6\cdot x\cdot\Delta x+3\cdot \Delta x^2}{\Delta x}=\lim_{\Delta x\rightarrow 0}6\cdot x+3\cdot \Delta x=6\cdot x
Pochodna funkcji c :
Zapis wyrażenia w formacie TeX-a:
f'(x)=\lim_{\Delta x\rightarrow 0}\frac{f\left(x+\Delta x\right) -f(x)}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{x+\Delta x+1-x-1}{\Delta x}=1
Pochodna funkcji d :
Zapis wyrażenia w formacie TeX-a:
f'(x)=\lim_{\Delta x\rightarrow 0}\frac{f\left(x+\Delta x\right) -f(x)}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{\sqrt{x+\Delta x}-\sqrt{x}}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{\sqrt{x+\Delta x}-\sqrt{x}}{\Delta x}\cdot\frac{\sqrt{x+\Delta x}+\sqrt{x}}{\sqrt{x+\Delta x}+\sqrt{x}}=\lim_{\Delta x
\rightarrow 0}\frac{x+\Delta x-x}{\Delta x\cdot\left(\sqrt{x+\Delta x}+\sqrt{x}\right)}=\lim_{\Delta x\rightarrow 0}\frac{1}{\sqrt{x+\Delta x}+\sqrt{x}}=\frac{1}{2\cdot \sqrt{x}}
Pochodna funkcji e :
Zapis wyrażenia w formacie TeX-a:
f'(x)=\lim_{\Delta x\rightarrow 0}\frac{f\left(x+Delta x\right) -f(x)}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{sin \left(x+\Delta x\right)-sin{x}}{\Delta x}
Do dalszych obliczeń konieczna jest znajomość wzoru [14] z działu Matematyka: Funkcje: Funkcje trygonometryczne . Ów wzór zostanie wykorzystany do rozpisania licznika ułamka funkcji pochodnej zapisanej powyżej.
Zapis wyrażenia w formacie TeX-a:
f'(x)=\lim_{\Delta x\rightarrow 0}\frac{2\cdot sin \left(\cfrac{x+\Delta x-x}{2}\right)\cdot cos\left(\cfrac{x+\Delta x+x}{2}
\right)}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{2\cdot sin \left(\cfrac{\Delta x}{2}\right)}{\Delta x}\cdot cos\left(x+\cfrac{\Delta x}{2}
\right)=\lim_{\Delta x\rightarrow 0}\frac{sin \left(\cfrac{\Delta x}{2}\right)}{\cfrac{\Delta x}{2}}\cdot cos\left(x+\cfrac{\Delta x}{2}\right)=1\cdot cos{x}=cos x
W analogiczny sposób należy postąpić w przypadku funkcji f , z tą tylko różnicą, że zastosowany tutaj jest wzór [15] z działu Matematyka: Funkcje: Funkcje trygonometryczne :
Zapis wyrażenia w formacie TeX-a:
f'(x)=\lim_{\Delta x\rightarrow 0}\frac{cos \left(x+\Delta x\right)-cos{x}}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{-2\cdot sin \left(\cfrac{x+\Delta x-x}{2}\right)\cdot sin\left(\cfrac{x+\Delta x+x}{2}\right)}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{-2\cdot sin \left(\cfrac{\Delta x}{2}\right)}{\Delta x}\cdot sin\left(x+\cfrac{\Delta x}{2}\right)=\lim_{\Delta x\rightarrow 0}-\frac{sin \left(\cfrac{\Delta x}{2}\right)}{\cfrac{\Delta x}{2}}\cdot sin\left(x+\cfrac{\Delta x}{2}\right)=-1\cdot sin{x}=-sin x Propozycje książek
Tytuł:
Matematyka w uczeniu maszynowym
Autor:
Marc Peter Deisenroth, A. Aldo Faisal, Cheng Soon Ong
Tytuł:
Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie
Autor:
Ryan T. White, Archana Tikayat Ray
Tytuł:
Matematyka w Pythonie. Algebra, statystyka, analiza matematyczna i inne dziedziny
Autor:
Amit Saha
Tytuł:
Matematyka dla menedżerów. Wydanie II
Autor:
Michael C. Thomsett
Tytuł:
Matematyka Poradnik encyklopedyczny
Autor:
I.N. Bronsztejn, K.A. Siemiendiajew
Tytuł:
Matematyka finansowa
Autor:
Jacek Jakubowski, Andrzej Palczewski, Marek Rutkowski, Łukasz Stettner
Tytuł:
Proste jak pi Matematyka to bułka z masłem
Autor:
Liz Strachan
Tytuł:
O twierdzeniach i hipotezach. Matematyka według Delty
Autor:
Witold Sadowski, Wiktor Bartol
Tytuł:
Matematyka dla biologów
Autor:
Dariusz Wrzosek
Tytuł:
Matematyka dla programistów Java
Autor:
Jacek Piechota