Twierdzenia o zbieżności ciągów liczbowych

Stronę tą wyświetlono już: 4451 razy

Twierdzenie o ciągach monotonicznych

Twierdzenie dla ciągów niemalejących

Każdy ciąg niemalejący i ograniczony z góry jest ciągiem zbieżnym.

Graficzna interpretacja tego twierdzenia została pokazana na poniższym rysunku, gdzie granicą ciągu niemalejącego (a_n) jest pewna liczba a, dla której dla dowolnego ε > 0 znajdzie się takie m ∈ N⁺, takie że każdy element o indeksie n ≥ m będzie spełniał nierówność a_m > a - ε.

Twierdzenie dla ciągów nierosnących

Każdy ciąg nierosnący i ograniczony z dołu jest ciągiem zbieżnym.

Twierdzenie Bolzano-Weierstrassa

Z każdego ciągu liczbowego ograniczonego można wybrać dowolny podciąg zbieżny.

Warunek Cauchy'ego zbieżności ciągów

Ciąg (a_n) jest zbieżny wtedy i tylko wtedy, gdy dla każdego ε > 0 i każdego n₀∈N⁺ każdy element ciągu o indeksie n>n₀ i m > n₀ spełnia warunek |a_n - a_m| < ε, co zapisuje się następująco:

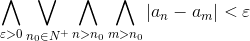[1]

Zapis wyrażenia w formacie TeX-a:

\bigwedge_{\varepsilon> 0}\bigvee_{n_0\in N^+}\bigwedge_{n> n_0}\bigwedge_{m> n_0}|a_n-a_m|<\varepsilon

Dla lepszego zrozumienia, niechaj dany będzie ciąg (a_n) następującej postaci:

[2]

Zapis wyrażenia w formacie TeX-a:

a_n=\frac{1}{n}

i ciąg (b_n), którego elementy składają się z wartości bezwzględnej z różnicy dwóch kolejnych elementów ciągu (a_n):

[3]

Zapis wyrażenia w formacie TeX-a:

b_n=|a_n-a_{n+1}|=\left|\frac{1}{n}-\frac{1}{n+1}\right|

to gdy ciąg (b_n) jest zbieżny (a w tym przypadku jest) to ciąg (a_n) też jest zbieżny.