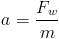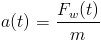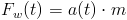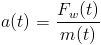II zasada dynamiki Newtona
Stronę tą wyświetlono już: 4112 razy
Druga zasada dynamiki Newtona:
Jeżeli na dane ciało działa pewna niezerowa siła wypadkowa Fw wtedy owe ciało porusza się ruchem jednostajnie przyspieszonym po linii prostej a nabyte przyspieszenie jest wprost proporcjonalne do działającej siły zaś odwrotnie proporcjonalne do masy m tego ciała.Z powyższej zasady wynika jednoznacznie, że gdy na dane ciało działa stała siła wypadkowa Fw owe ciało porusza się ruchem jednostajnie przyspieszonym a więc jeżeli siła ta zmienia się w czasie, wtedy to przyspieszenie zmienia się również w funkcji czasu. Zatem prawdziwa jest równość następująca:
Gdy dana jest więc funkcja a(t) oraz masa m poruszającego się obiektu wtedy to możliwe jest wyznaczenie funkcji Fw(t) w następujący sposób:
Również masa m obiektu może być zależna od czasu t, dla przykładu rakieta wystrzelona w kosmos zmienia w znacznym stopniu swoją masę w trakcie lotu spalając paliwo znajdujące się na jej pokładzie (pomijam tutaj fakt, że opróżnione z paliwa zbiorniki paliwowe zostają odłączane od rakiety w trakcie jej lotu). W myśl owej zasady można zapisać następującą zależność:
Oczywistym jest mam nadzieję fakt, że masa danego obiektu nie może być mniejsza ni równa zero, a więc funkcja m(t) nie może przyjmować wartości zerowych jak i ujemnych w zadanym przedziale czasu t.
Siła jest więc przyczyną każdego ruchu, albowiem raz przyłożona do danego obiektu wprawia go w ruch jednostajnie przyspieszony zaś po zakończeniu jej oddziaływania lub jej zrównoważeniu przez inne siły pozostawia ciało w ruchu jednostajnym prostoliniowym.
Oddziaływanie siły zewnętrznej może również zmieniać tor ruchu danego obiektu, ale to jest temat który zostanie poruszony w innym dziale.