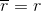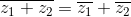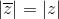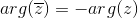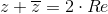Stronę tą wyświetlono już: 5650 razy

Sprzężenie liczby zespolonej z jest to liczba zespolona, której wartość jest odbiciem lustrzanym liczby z. Graficzna interpretacja tego zawiłego zagadnienia pokazana została na poniższym rysunku.

Sprzężenie zwrotne liczby:

[1]

Zapis wyrażenia w formacie TeX-a:

z=a+bi

jest więc równe:

[2]

Zapis wyrażenia w formacie TeX-a:

\overline{z}=a-bi

Właściwości sprzężenia zwrotnego liczby zespolonej:

• sprzężenie zwrotne liczby rzeczywistej jest równe tej liczbie:

  [3]

  Zapis wyrażenia w formacie TeX-a:

  \overline{r}=r

• sprzężenie sumy liczb zespolonych jest równe sumie sprzężeń tychże liczb:

  [4]

  Zapis wyrażenia w formacie TeX-a:

  \overline{z_1+z_2}=\overline{z_1}+\overline{z_2}

• Moduł sprzężenia jest równy modułowi liczby zespolonej:

  [5]

  Zapis wyrażenia w formacie TeX-a:

  |\overline{z}|=|z|

• kąt zawarty pomiędzy osią liczb rzeczywistych a sprzężeniem liczby jest taki sam jak w przypadku liczby zespolonej lecz ma przeciwny znak. Ów kąt nazywany jest argumentem liczby zespolonej:

  [6]

  Zapis wyrażenia w formacie TeX-a:

  arg(\overline{z})=-arg(z)

• suma liczby zespolonej i sprzężenia tej liczby jest liczbą rzeczywistą równą:

  [7]

  Zapis wyrażenia w formacie TeX-a:

  z+\overline{z}=2\cdot Re
• jeżeli część rzeczywista liczby zespolonej jest równa zero to sprzężenie zwrotne takiej liczby jest jej odwrotnością.

• jeżeli liczba zespolona jest pierwiastkiem wielomianu rzeczywistego to sprzężenie takiej liczby również jest pierwiastkiem tegoż wielomianu.