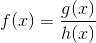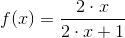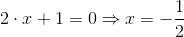Asymptota pionowa funkcji

Autor podstrony: Krzysztof Zajączkowski

Stronę tą wyświetlono już: 5523 razy

A niechaj będzie funkcja f(x), taka że:

Zapis wyrażenia w formacie TeX-a:

f(x)=\frac{g(x)}{h(x)}

to miejsca zerowe podfunkcji h(x) wchodzącej w skład funkcji f(x) wyznaczają miejsce nieciągłości funkcji a tym samym miejsce wystąpienia asymptoty pionowej funkcji f(x). Dzieje się tak albowiem wiadomo powszechnie, że im mniejsza jest wartość w mianowniku tym większa liczba. Tak więc przy h(x)=0 stosunek g(x) do h(x) jest równy nieskończoności.

Typowym przykładem funkcji tego typu są funkcje wymierne. Oto przykład:

[2]

Zapis wyrażenia w formacie TeX-a:

f(x)=\frac{2 \cdot x}{2 \cdot x + 1}

Jak pisałem, miejsce zerowe funkcji znajdującej się w mianowniku wyznacza miejsce wystąpienia asymptoty poziomej. Tak więc szukany jest taki x, dla którego:

[3]

Zapis wyrażenia w formacie TeX-a:

2 \cdot x + 1 = 0\Rightarrow x = -\frac{1}{2}

Jak widać w tym przypadku funkcja f(x) ma asymptotę poziomą dla x = -0.5.

Rys. 1

Wykres funkcji f(x), gdzie jak widać w punkcie x = -0.5 znajduje się asymptota pozioma tejże funkcji

Źródło:

Wykres wygenerowany przez skrypt PHP autora strony opisany na stronie Programowanie → Skrypty PHP → Skrypt PHP generujący wykres funkcji 2W

Również funkcje trygonometryczne takie jak tangens czy kotangens mają swoje asymptoty poziome, gdyż funkcje te stanowią stosunek dwóch innych funkcji trygonometrycznych. W przypadku tych funkcji asymptota pozioma pojawia się cyklicznie co 2·π radianów.