Punkt przegięcia funkcji
Stronę tą wyświetlono już: 10090 razy
Czym jest punkt przegięcia funkcji
Zanim przejdę do tego jak sprawdzić, czy dana funkcja ma punkt przegięcia, najpierw pokażę graficznie jakie warunki taki punk przegięcia musi spełniać. W tym celu weźmy sobie taki oto prosty wielomian trzeciego stopnia:
Użyję teraz wzoru [4] z strony Matematyka → Pochodna funkcji → Wzór prostej stycznej do funkcji, by uzyskać następujący wzór funkcji stycznej do punktu przegięcia funkcji f(x):
Teraz rzućmy łaskawym okiem na wykres tej funkcji w otoczeniu punktu przegięcia, który wiem z pewnych źródeł, że znajduje się w punkcie x= -1/3.
I teraz na podstawie powyższego wykresu mogę wytłumaczyć czym jest punkt przegięcia. Jeżeli obrany zostanie jakiś punkt na wykresie funkcji i narysowana zostanie styczna do tej funkcji w danym punkcie xs i jeżeli się tak szczęśliwie złoży, iż najbliższe otoczenie wykresu tej funkcji po jednej stronie punktu xs; f(xs) i po drugiej stronie tegoż punktu będzie znajdować się po przeciwnych stronach stycznej, to taki punkt jest punktem przegięcia funkcji f(x).
Punkt przegięcia wyznacza więc pewną granicę, pomiędzy częścią wklęsłą wykresu funkcji f(x) a częścią wypukłą.
Warunki istnienia punktu przegięcia funkcji
Funkcja w otoczeniu punktu przegięcia musi być ciągła i musi być co najmniej dwukrotnie różniczkowalna. Jeżeli jednak funkcja ta jest różniczkowalna trzykrotnie to można skorzystać z warunku mówiącego, że: jeżeli funkcja f(x) jest różniczkowalna potrójnie i druga pochodna f''(x) ma miejsce zerowe w pewnym punkcie xp oraz trzecia pochodna f'''(x) w tymże punkcie nie jest równa 0 to punkt xp jest punktem przegięcia funkcji f(x).
No to nie pozostało nic innego jak sprawdzić, czy funkcja [1] rzeczywiście ma punkt przegięcia. Najpierw trzeba wyznaczyć pierwszą pochodną tej funkcji:
Druga pochodna funkcji f(x):
Jak widać druga pochodna istnieje i ma się dobrze, a jej miejsce zerowe to x = -1/3. No to pozostało obliczenie trzeciej pochodnej:
Jak widać trzecia pochodna istnieje i jest różna od zera w punkcie x = -1/3 a więc punkt -1/3; f(x=-1/3) jest punktem przegięcia.
Można sobie też darować obliczanie trzeciej pochodnej i sprawdzić, czy druga pochodna w otoczeniu jej miejsca zerowego zmienia znak po jednej stronie na przeciwny po drugiej jego stronie.

Tytuł:
Matematyka w uczeniu maszynowym
Autor:
Marc Peter Deisenroth, A. Aldo Faisal, Cheng Soon Ong

Tytuł:
Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie
Autor:
Ryan T. White, Archana Tikayat Ray

Tytuł:
Matematyka w Pythonie. Algebra, statystyka, analiza matematyczna i inne dziedziny
Autor:
Amit Saha

Tytuł:
Matematyka dla menedżerów. Wydanie II
Autor:
Michael C. Thomsett

Tytuł:
Matematyka Poradnik encyklopedyczny
Autor:
I.N. Bronsztejn, K.A. Siemiendiajew

Tytuł:
Matematyka finansowa
Autor:
Jacek Jakubowski, Andrzej Palczewski, Marek Rutkowski, Łukasz Stettner

Tytuł:
Proste jak pi Matematyka to bułka z masłem
Autor:
Liz Strachan

Tytuł:
O twierdzeniach i hipotezach. Matematyka według Delty
Autor:
Witold Sadowski, Wiktor Bartol

Tytuł:
Matematyka dla biologów
Autor:
Dariusz Wrzosek

Tytuł:
Matematyka dla programistów Java
Autor:
Jacek Piechota

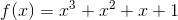
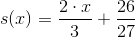
![Pierwsza pochodna funkcji f('x) (wzór [1])](https://obliczeniowo.com.pl/rownania/w_2819.gif)
![Druga pochodna funkcji f''(x) (wzór [1])](https://obliczeniowo.com.pl/rownania/w_2820.gif)
![Trzecia pochodna funkcji f'''(x) (wzór [1])](https://obliczeniowo.com.pl/rownania/w_2821.gif)