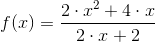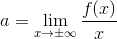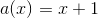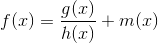Asymptota ukośna funkcji

Stronę tą wyświetlono już: 2510 razy

Dana funkcja f(x) ma asymptotę ukośną opisaną funkcją liniową postaci y(x)=a·x+b wtedy i tylko wtedy, gdy granica pochodnej tejże funkcji dla x→+∞ lub dla x→-∞ jest wartością liczbową, która określa jednocześnie wartość współczynnika a funkcji asymptoty ukośnej.

Dla przykładu funkcja:

[1]

Zapis wyrażenia w formacie TeX-a:

f(x)=\frac{2\cdot x^2+4\cdot x}{2\cdot x+2}

ma pochodną:

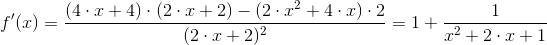[2]

Zapis wyrażenia w formacie TeX-a:

f'(x)=\frac{(4\cdot x+4)\cdot(2\cdot x+2)-(2\cdot x^2+4\cdot x)\cdot 2}{(2\cdot x+2)^2}=1+\frac{1}{x^2+2\cdot x+1}

tak więc granica tejże pochodnej dla x→∞ wynosi:

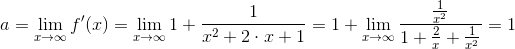[3]

Zapis wyrażenia w formacie TeX-a:

a=\lim_{x\rightarrow \infty}f'(x)=\lim_{x\rightarrow \infty}1+\frac{1}{x^2+2\cdot x+1}=1+\lim_{x\rightarrow \infty}\frac{\frac{1}{x^2}}{1+\frac{2}{x} + \frac{1}{x^2}}=1

Z powyższego wynika, że współczynnik a będzie równy 1. Współczynnik ten można również wyliczyć w nieco prostszy sposób stosując wzór:

[4]

Zapis wyrażenia w formacie TeX-a:

a=\lim_{x\rightarrow \pm \infty}\frac{f(x)}{x}

Obliczenie współczynnika b polega z kolei na obliczeniu następującej granicy:

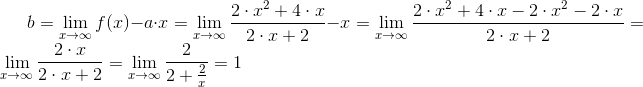[5]

Zapis wyrażenia w formacie TeX-a:

b=\lim_{x\rightarrow \infty}f(x)-a\cdot x=\lim_{x\rightarrow \infty}\frac{2\cdot x^2+4\cdot x}{2\cdot x+2}-x=\lim_{x\rightarrow \infty}\frac{2\cdot x^2+4\cdot x - 2\cdot x^2 - 2\cdot x}{2\cdot x+2}=\lim_{x\rightarrow \infty}\frac{2\cdot x}{2\cdot x+2}=\lim_{x\rightarrow \infty}\frac{2}{2+\frac{2}{x}}=1

Tak więc ostatecznie wzór asymptoty funkcji f(x) będzie następujący:

[6]

Zapis wyrażenia w formacie TeX-a:

a(x)=x + 1

Wykres funkcji f(x) oraz asymptoty ukośnej pokazany został na poniższej ilustracji.

Ktoś mógłby mi zarzucić, że nie policzyłem granic dla x→-∞, tą część zadania pozostawiam do rozwiązania samodzielnego czytelnikowi.

Funkcje, które mają asymptotę ukośną najczęściej dają się doprowadzić do postaci następującej:

[7]

Zapis wyrażenia w formacie TeX-a:

f(x)=\frac{g(x)}{h(x)}+m(x)

gdzie m(x) jest funkcją liniową powodującą pochylenie asymptoty.

Tytuł:

Matematyka dyskretna dla praktyków. Algorytmy i uczenie maszynowe w Pythonie

Autor:

Ryan T. White, Archana Tikayat Ray

Tytuł:

Matematyka w Pythonie. Algebra, statystyka, analiza matematyczna i inne dziedziny

Autor:

Amit Saha

Tytuł:

Matematyka dla menedżerów. Wydanie II

Autor:

Michael C. Thomsett

Tytuł:

Matematyka Poradnik encyklopedyczny

Autor:

I.N. Bronsztejn, K.A. Siemiendiajew

Tytuł:

Matematyka finansowa

Autor:

Jacek Jakubowski, Andrzej Palczewski, Marek Rutkowski, Łukasz Stettner

Tytuł:

Sprawdziany Matematyka Klasa 3

Autor:

Iwona Kowalska, Beata Guzowska

Tytuł:

Proste jak pi Matematyka to bułka z masłem

Autor:

Liz Strachan

Tytuł:

O twierdzeniach i hipotezach. Matematyka według Delty

Autor:

Witold Sadowski, Wiktor Bartol

Tytuł:

Matematyka dla biologów

Autor:

Dariusz Wrzosek

Tytuł:

Matematyka dla programistów Java

Autor:

Jacek Piechota

Komentarze