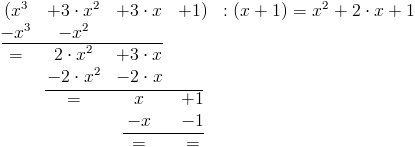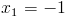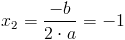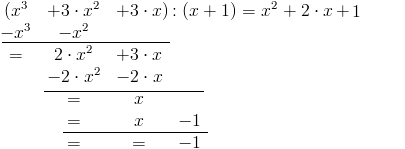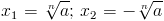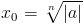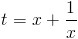Stronę tą wyświetlono już: 6613 razy

Wielomianem nazywa się każdą funkcję postaci:

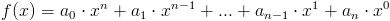[1]

Zapis wyrażenia w formacie TeX-a:

f(x)=a_0\cdot x^n+a_1\cdot x^{n-1}+...+a_{n-1}\cdot x^1+a_n\cdot x^0

gdzie:

• a₁, a₂,...,a_n-1,a_n - parametry liczbowe wielomianu
• n - stopień wielomianu n∈N

Szczególną postacią wielomianów są funkcje liniowe (wielomiany 1-go stopnia) oraz funkcje kwadratowe (wielomiany 2-go stopnia).

Podzielność wielomianu

Dany wielomian f(x) jest podzielny przez wielomian g(x), który nie jest równy tożsamościowo 0 wtedy i tylko wtedy, gdy istnieje wielomian h(x) taki, że f(x)=g(x)⋅h(x).

Z powyższego zapisu wynika, że pierwiastki wielomianów g(x) oraz h(x) są również pierwiastkami wielomianu f(x). Tak więc powyższe twierdzenie może stać się pomocne przy wyznaczaniu pierwiastków wielomianu f(x).<

Przykład

Dane są wielomiany f(x)=x³+3⋅x²+3⋅x+1 oraz g(x)=x+1, takie że wielomian f(x) podzielony przez wielomian g(x) daje w wyniku wielomian h(x) wyznaczone w następujący sposób:

Pierwiastki wielomianu g(x):

Pierwiastek wielomianu h(x), dla którego wyróżnik Δ=0 jest równy:<

Jedynym więc pierwiastkiem wielomianu f(x) jest x=-1.

Dla każdego dzielenia wielomianu f(x) przez wielomian g(x), taki że g(x) nie jest równy tożsamościowo 0, istnieją takie dwa wielomiany h(x), r(x), takie że spełniona jest następna równość: f(x)=g(x)⋅h(x)+r(x), przy czym wielomian r(x) jest równy tożsamościowo 0, gdy f(x) dzieli się bez reszty przez wielomiany g(x), h(x) lub jest wielomianem mniejszego stopnia od wielomianu g(x).

Przykład

Dane są dwa wielomiany f(x)=x³+3⋅x²+3⋅x, g(x)=x+1, takie że wielomian f(x) podzielony przez wielomian g(x) daje w wyniku wielomiany h(x), r(x) wyznaczone w następujący sposób:

gdzie:

• x²+2⋅x+1 - wielomian h(x);
• -1 - wielomian r(x) (reszta z dzielenia)

Własności wielomianów

Wielomiany stopnia nieparzystego mają co najmniej jedno miejsce zerowe a ich przeciwdziedzina zawiera się w przedziale od -∞ do ∞.

Każdy wielomian może mieć co najwyżej n rzeczywistych rozwiązań, gdzie n jest stopniem danego wielomianu.

Wielomiany stopnia parzystego mają przeciwdziedzinę zawierającą się w przedziale od minimum globalnego do ∞, gdy parametr a₀>0, natomiast w przedziale od -∞ do maksimum globalnym gdy parametr a₀<0.

Każdy wielomian parzysty postaci xⁿ-a ma dwa rzeczywiste rozwiązania:

natomiast dla stopnia parzystego tej samej postaci istnieje jedno rozwiązanie:

Każdy wielomian, którego wyraz wolny a_n=0 ma miejsce zerowe w początku układu współrzędnych.

Twierdzenie Bézouta

Liczba r jest pierwiastkiem wielomianu f(x) wtedy i tylko wtedy, gdy wielomian f(x) jest podzielny przez dwumian x-r.

Reszta z dzielenia wielomianu f(x) przez dwumian x-a jest równa f(x=a).

Twierdzenia o pierwiastkach wielomianu o współczynnikach całkowitych

Jeżeli liczba całkowita r≠0 jest pierwiastkiem wielomianu f(x) o współczynnikach całkowitych, to jest ona dzielnikiem wyrazu wolnego a_n.

Jeżeli nieskracalny ułamek p/q, gdzie p, q∈C i q≠0 jest pierwiastkiem wielomianu f(x) o współczynnikach całkowitych, to licznik p jest dzielnikiem wyrazu wolnego a_n, a mianownik q jest dzielnikiem współczynnika a₀.

Twierdzenia o rozkładzie wielomianów

Jeżeli liczby x₁, x₂,....,x_k są pierwiastkami wielomianu f(x) to f(x)=a₀⋅(x-x₁)⋅(x-x₂)⋅...⋅(x-x_k), gdzie k jest mniejsze lub równe stopniowi wielomianu f(x).

Każdy wielomian f(x) nie równy tożsamościowo 0 jest iloczynem czynników stopnia co najwyżej drugiego.

Pierwiastek wielokrotny

Liczbę r nazywamy k-krotnym pierwiastkiem wielomianu f(x) stopnia n gdzie k, n∈N i k≤n wtedy i tylko wtedy, gdy wielomian f(x) jest podzielny przez (x-r)^k i nie jest podzielny przez (x-r)^k+1.

Liczba r jest k-krotnym pierwiastkiem wielomianu f(x), wtedy i tylko wtedy, gdy f(x)=f'(x)=...=f^(k-1)(x) i f^k(x)≠0, gdzie f^k(x) jest k-tą pochodną wielomianu f(x).

Metody wyznaczania miejsc zerowych niektórych wielomianów stopnia wyższego niż 2

Wielomiany dające się uprościć do postaci równania kwadratowego

Wielomian f(x)=a⋅x^2⋅n+b⋅xⁿ+c=0, gdzie a≠0 można uprościć do postaci równania kwadratowego poprzez zastosowanie zmiennej pomocniczej t=xⁿ, gdzie z kolei t≥0, gdy n jest liczbą parzystą.

W takim przypadku rozwiązuje się równanie kwadratowe f(t)=a⋅t²+b⋅t+c w sposób opisany już w wcześniejszym rozdziale.

Wielomian zwrotny czwartego stopnia

Wielomian postaci f(x)=a⋅x⁴+b⋅x³+b⋅x²+b⋅x+1 można rozwiązać poprzez wstępne podzielenie wielomianu f(x) przez x² otrzymując następującą postać wielomianu f(x):

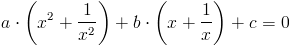Zapis wyrażenia w formacie TeX-a:

a\cdot \left(x^2+\frac{1}{x^2}\right)+b\cdot\left(x+\frac{1}{x}\right)+c=0

a następnie podstawiając następującą zmienną pomocniczą:

otrzymując w ten jakże przebiegły sposób zwyczajne równanie kwadratowe f(t)=a⋅t²+b⋅t+c.

Równanie algebraiczne stopnia n

Jeżeli wielomian f(x)=a₀⋅xⁿ+a₁⋅x^n-1+...+a_n-1⋅x¹+a_n⋅x⁰ rozkłada się na czynniki a_n⋅ (x-x₁)⋅(x-x₂)⋅...⋅(x-x_n-1)⋅(x-x_n), gdzie a₀≠0, to równanie f(x)=0 jest równoważne alternatywie równań: x-x₁=0 ∨ x-x₂=0 ∨ ... ∨ x-x_n-1=0 ∨ x-x_n=0