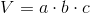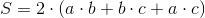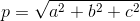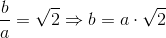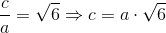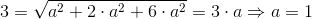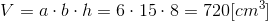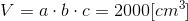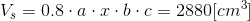Prostopadłościany

Autor podstrony: Krzysztof Zajączkowski

Stronę tą wyświetlono już: 8188 razy

Prostopadłościany to ogólnie mówiąc sześciany, których boki składają się z prostokątów. Szczególnym przypadkiem prostopadłościanu jest sześcian foremny lub sześcian Platoński. Kąt zawarty pomiędzy sąsiadującą parą ścian prostopadłościanu są sobie równe i wynoszą 90°. Każdy prostopadłościan ma:

4 przekątne;
6 ścian;
8 wierzchołków;
8 krawędzi;

Podstawowe wzory:

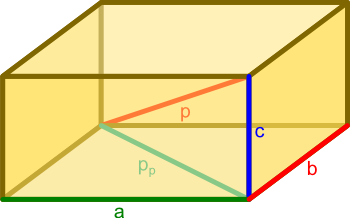
Ilustracja prostopadłościanu wraz z jego oznaczeniami — Rys. 1
Ilustracja **prostopadłościanu** wraz z jego oznaczeniami:
a, b, c - długości krawędzi **prostopadłościanu**;

p - jedna z przekątnych **prostopadłościanu**;

**p_p** - przekątna podstawy **prostopadłościanu**

Objętość prostopadłościanu:

[1]

Zapis wyrażenia w formacie TeX-a:

V=a\cdot b\cdot c

Pole powierzchni prostopadłościanu:

Wzór na pole powierchni bocznych prostopadłościanu

[2]

Zapis wyrażenia w formacie TeX-a:

S=2\cdot(a\cdot b+b\cdot c+a\cdot c)

Długość przekątnej prostopadłościanu:

[3]

Zapis wyrażenia w formacie TeX-a:

p=\sqrt{a^2+b^2+c^2}

Promień kuli opisanej na prostopadłościanie:

[4]

Zapis wyrażenia w formacie TeX-a:

R=\frac{p}{2}=\frac{\sqrt{a^2+b^2+c^2}}{2}

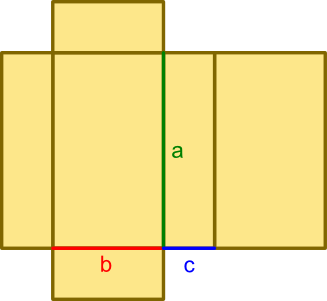
Przykładowa siatka prostopadłościanu

Zadania

Zadanie 1

Oblicz objętość prostopadłościanu, którego przekątna p = 3 [cm] zaś stosunek długości boku b do a jest równy 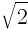sqrt{2} oraz stosunek boku c do a wynosi sqrt{6} .

Pomocniczy rysunek prostopadłościanu do zadania 1 — Rys. 3
Rysunek pomocniczy.

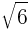Do rozwiązania tego zadania konieczne będzie skorzystanie z wzoru [3], ale zanim to nastąpi najpierw trzeba uzależnić długości boków prostopadłościanu tak, aby w równaniu [3] pozostała tylko jedna niewiadoma. Oto przekształcenia:

$frac{b}{a}=sqrt{2}Rightarrow b=acdotsqrt{2}$

[5]

Zapis wyrażenia w formacie TeX-a:

\frac{b}{a}=\sqrt{2}\Rightarrow b=a\cdot\sqrt{2}

$frac{c}{a}=sqrt{6}Rightarrow c=acdotsqrt{6}$

[6]

Zapis wyrażenia w formacie TeX-a:

\frac{c}{a}=\sqrt{6}\Rightarrow c=a\cdot\sqrt{6}

Do równania [3] podstawić należy w następujący sposób:

$3=sqrt{a^2+2cdot a^2+ 6cdot a^2}=3cdot aRightarrow a = 1$

[7]

Zapis wyrażenia w formacie TeX-a:

3=\sqrt{a^2+2\cdot a^2+ 6\cdot a^2}=3\cdot a\Rightarrow a = 1

Znając a można obliczyć objętość prostopadłościanu:

$V=acdot acdotsqrt{2}cdot acdotsqrt{6}= sqrt{12} = 2cdotsqrt{3},[cm^3]$

[8]

Zapis wyrażenia w formacie TeX-a:

V=a\cdot a\cdot\sqrt{2}\cdot a\cdot\sqrt{6}= \sqrt{12} = 2\cdot\sqrt{3}\,[cm^3]

Zadanie 2

Oblicz objętość prostopadłościanu, którego przekątna jednej powierzchni bocznej p₁ = 10[cm] zaś drugiej powierzchni bocznej p₂ = 17[cm] natomiast wysokość h tego sześcianu będąca równocześnie krawędzią obu tych boków ma długość 8[cm].

Pomocniczy rysunek prostopadłościanu do zadania 2 — Rys. 4
Rysunek pomocniczy.

Korzystając z starego dobrego twierdzenia Pitagorasa można obliczyć długość boku a i b, co też i z najdzikszą rozkoszą czynię:

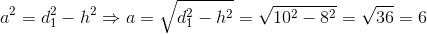[9]

Zapis wyrażenia w formacie TeX-a:

a^2=d_1^2-h^2\Rightarrow a=\sqrt{d_1^2-h^2}=\sqrt{10^2-8^2}=\sqrt{36}=6

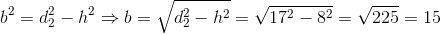[10]

Zapis wyrażenia w formacie TeX-a:

b^2=d_2^2-h^2\Rightarrow b=\sqrt{d_2^2-h^2}=\sqrt{17^2-8^2}=\sqrt{225}=15

Skoro znane są długości wszystkich krawędzi prostopadłościanu to pozostało już tylko obliczenie upragnionej objętości:

[11]

Zapis wyrażenia w formacie TeX-a:

V=a\cdot b\cdot h=6\cdot 15\cdot 8=720 [cm^3]

Zadanie 3

Dany jest prostopadłościan o bokach a, b i c i objętości V = 3000 [m³], który po skróceniu najkrótszego boku o 20% i wydłużeniu najdłuższego ma objętość V₂ = 2880 [m³]. Oblicz o ile procent wydłużył się najdłuższy bok tego prostopadłościanu.

Dane jest więc:

objętość sześcianu przed zmianą długości boków

[12]

Zapis wyrażenia w formacie TeX-a:

V=a\cdot b\cdot c=2000 [cm^3]

oraz:

objętość sześcianu po zmianie długości boków

[13]

Zapis wyrażenia w formacie TeX-a:

V_s=0.8\cdot a\cdot x \cdot b\cdot c=2880 [cm^3]

Po podstawieniu za a·b·c zależności [12] otrzymuje się następujące równanie z jedną niewiadomą:

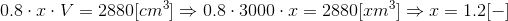Wyznaczanie skrócenia boku prostopadłościanu

[14]

Zapis wyrażenia w formacie TeX-a:

0.8\cdot x \cdot V=2880 [cm^3]\Rightarrow 0.8\cdot 3000\cdot x = 2880 [xm^3]\Rightarrow x=1.2 [-]

Z powyższego wynika, że długość najdłuższego boku prostopadłościanu została zwiększona o 20%.