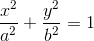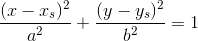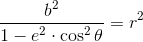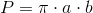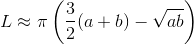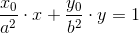Elipsa
Stronę tą wyświetlono już: 36373 razy
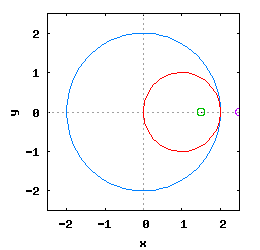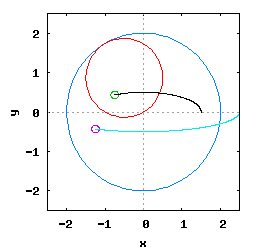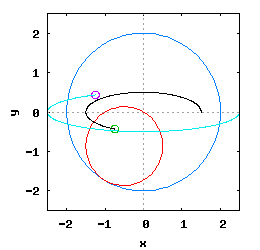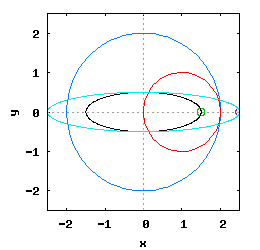
Podstawowa definicja i oznaczenia
A niechaj będą dane dwa punkty F1 i F2 takie, że F1 ≠ F2, które są ogniskami elipsy i dwie dodatnie liczby rzeczywiste a i b, które z kolei opisują wartości promieni tejże elipsy, to w takim przypadku zbiór wszystkich punktów, których suma odległości od ognisk elipsy F1 i F2 jest stała i wynosi 2· a, gdzie z kolei 2·a > |F1F2|=2· c > 0.
- S - środek ciężkości elipsy;
- A1, A2, B1, B2 - punkty charakterystyczne elipsy, wyznaczające największą 2·a i najmniejszą 2·b jej średnicę;
- a - promień maksymalny elipsy;
- b - promień minimalny elipsy;
- F1, F2 - ogniskowe elipsy;
- R1, R2 - promienie wodzące punktu P;
- P - punkt na obwodzie elipsy;
- P1 - rzut punktu P na prowadnicę k1;
- k, l - osie symetrii elipsy;
- k1, k2 - prowadnice elipsy
Patrząc na powyższą ilustrację i stosując się do definicji elipsy należy stwierdzić niezbicie, że dla dowolnie obranego punktu P znajdującego się na obwodzie elipsy można zapisać następującą równość:
Odległość c ogniskowych F1 i F2 od środka ciężkości S elipsy można wyznaczyć wykorzystując następujący wzór:
Elipsę charakteryzuje również pewna wartość e nazywana mimośrodem elipsy, która jest równa:
Dla każdego punktu P elipsy spełniona jest następująca równość powiązana z mimośrodem e:
gdzie:
- |P, k1| - odległość punktu P od prowadnicy k1;
- |P, k2| - odległość punktu P od prowadnicy k2;
Odległość położenia prowadnic k1, k2 na osi symetrii symetrii k od środka ciężkości S można obliczyć z następującej zależności:
Równanie elipsy
Dla elipsy, której środek ciężkości S znajduje się w początku układu współrzędnych równanie będzie przyjmowało następującą postać
gdzie a > 0 i b > 0.
Natomiast dla elipsy, dla której środek ciężkości S = {xs, ys} równanie to przyjmuje postać następującą:
Równania parametryczne elipsy dla parametru t, takiego że ) ≤ t ≤ 2 · π:
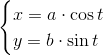 | [8] |
Zapis wyrażenia w formacie TeX-a:
W układzie współrzędnych biegunowych, równanie elipsy wygląda następująco:
Elipsa jako szczególny przypadek hipocykloidy
Istnieje szczególny przypadek Hipocykloid, które są w stanie wykreślić krzywe eliptyczne co zostało pokazane na poniższej animacji. Więcej informacji na temat tego typu krzywych można zobaczyć na stronie Matematyka → Geometria → Hipocykloidy.
Klatki do powyższej animacji zostały wykonane w programie wxMaxima, natomiast poskładane zostały w programie Gimp
Konstrukcje kreślenia elips
Na stronie Geometria wykreślna → Podstawowe konstrukcje → Kreślenie elips zostały pokazane i omówione dość szczegółowo najczęściej stosowane konstrukcje umożliwiające przybliżone kreślenie krzywych eliptycznych. Same ilustracje tychże metod zostały zamieszczone na poniższym rysunku.
Kreślenie elipsy za pomocą dwóch szpilek, sznurka i ołówka
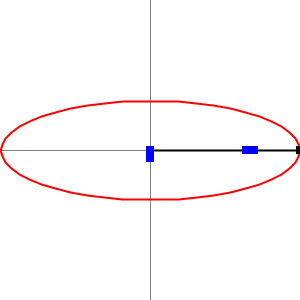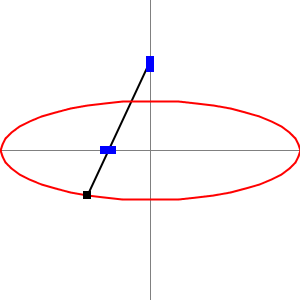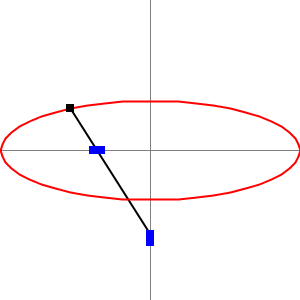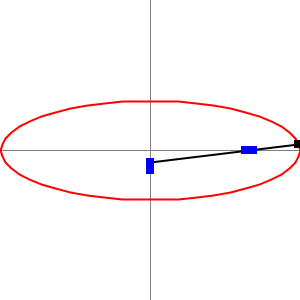
Na poniższej ilustracji punkty F1 i F2 stanowią miejsce wbicia szpilek, do których należy przywiązać sznurek. Ten z kolei będzie ograniczał ruch ołówka co umożliwi wykreślenie przybliżonej elipsy.
Kreślenie elipsy za pomocą elipsografu
Elipsograf to dość zmyślny przyrząd wykorzystujący parę suwadeł i cięgno do kreślenia elipsy bez konieczności stosowania jakichkolwiek metod interpolacyjnych (np. przy użyciu krzywików). Zasada działania takiego przyrządu pokazana została na poniższej animacji.
Pole powierzchni i obwód elipsy
Pole powierzchni elipsy można obliczyć za pomocą następującego wzoru:
Przybliżony obwód elipsy można obliczyć za pomocą następującego wzoru:
Dokładny wzór:
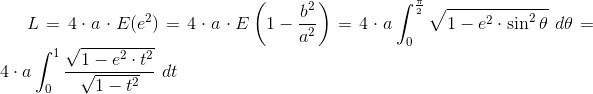 | [12] |
Zapis wyrażenia w formacie TeX-a:
gdzie:
- E - to zupełna całka eliptyczna drugiego rodzaju;
- e - mimośród elipsy
Równanie stycznej do elipsy
Gdy elipsa ma środek ciężkości w początku układu współrzędnych, to równanie prostej stycznej do punktu P0 = {x0, y0} to równanie przyjmuje następującą postać:
W przypadku, gdy środek ciężkości elipsy nie znajduje się w początku układu współrzędnych równanie stycznej przyjmuje postać:
 | [14] |
Zapis wyrażenia w formacie TeX-a:
Właściwości stycznych do elipsy
Każda styczna do elipsy stanowi dwusieczną kąta zewnętrznego (co pokazano na poniższej ilustracji).
Jeżeli dane są dwie styczne do punktów P1 i P2 elipsy oraz punkt przecięcia P3 tychże stycznych, to kąt zawarty pomiędzy jedną z ogniskowych a punktem P1 i P3 oraz P2 i P3 są sobie równe, co zostało pokazane na poniższej ilustracji.

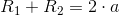
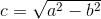
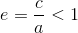
![Równanie [4]](https://obliczeniowo.com.pl/rownania/w_2840.gif)
![Równanie [5]](https://obliczeniowo.com.pl/rownania/w_2841.gif)